题目内容
抛物线x=-4y2的焦点坐标是 .
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先把抛物线整理标准方程,进而可判断出焦点所在的坐标轴和p,进而求得焦点坐标.
解答:
解:整理抛物线方程得y2=-
x,
∴焦点在x轴,p=
,∴焦点坐标为(-
,0)
故答案为:(-
,0).
| 1 |
| 4 |
∴焦点在x轴,p=
| 1 |
| 8 |
| 1 |
| 16 |
故答案为:(-
| 1 |
| 16 |
点评:本题主要考查了抛物线的简单性质.求抛物线的焦点时,注意抛物线焦点所在的位置,以及抛物线的开口方向.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若直线(2a+b)x+y-1=0(a>0,b>0)经过椭圆
+
=1的右焦点,则
+
的最小值是( )
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| a |
| 1 |
| b |
A、
| ||
| B、4 | ||
C、3+2
| ||
| D、6 |
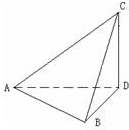 如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是
如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是