题目内容
6.已知双曲线C的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),若C的右支上存在两点A、B,使∠AOB=120°,其中O为坐标原点,则曲线C的离心率的取值范围是(2,+∞).分析 求出双曲线的渐近线方程,由题意可得$\frac{b}{a}$>tan60°=$\sqrt{3}$,由a,b,c的关系和离心率公式,计算即可得到所求范围.
解答 解:由C的右支上存在两点A、B,使∠AOB=120°,
而渐近线方程为y=±$\frac{b}{a}$x,
可得$\frac{b}{a}$>tan60°=$\sqrt{3}$,
即为b>$\sqrt{3}$a,即为b2>3a2,
即c2-a2>3a2,
即有c2>4a2,
即c>2a,
e=$\frac{c}{a}$>2,
故答案为:(2,+∞).
点评 本题考查双曲线的离心率的求法,注意运用双曲线的渐近线方程,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
16.命题“?x0∈R,$\frac{2}{{x}_{0}}$+lnx0≤0”的否定是( )
| A. | ?x∈R,$\frac{2}{x}$+lnx>0 | B. | ?x∈R,$\frac{2}{x}$+lnx≥0 | ||
| C. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0<0 | D. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0>0 |
17.已知简单组合体的三视图如图所示,则此简单组合体的体积为( )
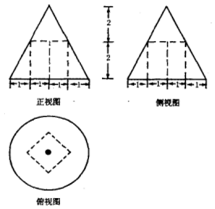

| A. | $\frac{10π}{3}-4$ | B. | $\frac{10π}{3}-8$ | C. | $\frac{16π}{3}-4$ | D. | $\frac{16π}{3}-8$ |
1.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,f($\frac{π}{2}$)=-1,则f(0)的值为( )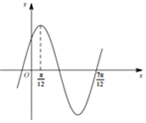

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
18.在△ABC中,BC=1且cosA=-$\frac{\sqrt{10}}{10}$,B=$\frac{π}{4}$,则BC边上的高等于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
15.已知数列{an}的各项均为正整数,其前n项和为Sn,an+1=$\left\{\begin{array}{l}{\frac{{a}_{n}+1}{2}{,a}_{n}是奇数}\\{{3a}_{n}-1{,a}_{n}是偶数}\end{array}\right.$,若S3=10,则S180=( )
| A. | 600或900 | B. | 900或560 | C. | 900 | D. | 600 |
5.已知全集为U=R,集合B={x|($\frac{1}{2}$)x≤1},A={x|x≥2},则(∁UA)∩B=( )
| A. | [0,2) | B. | [0,2] | C. | (1,2) | D. | (1,2] |