题目内容
16.设a=log${\;}_{\frac{1}{2}}$3,b=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$,c=2${\;}^{\frac{1}{3}}$,则( )| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c? |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵a=log${\;}_{\frac{1}{2}}$3<0,b=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$∈(0,1),c=2${\;}^{\frac{1}{3}}$>1,
∴a<b<c.
故选:A.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}4\;|{\;{{log}_2}x\;}|\;\;\;\;\;0<x<2\\ \frac{1}{2}{x^2}-5x+12\;\;\;\;\;x≥2\end{array}$,若存在实数a,b,c,d满足f(a)=f(b)=f(c)=f(d),若d>c>b>a>0,则abc(d-4)的取值范围是( )
| A. | (8,9) | B. | (8,9] | C. | (12,32) | D. | [12,32) |
4.若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x)<0的解集是( )
| A. | (-1,0) | B. | (-∞,-1)∪(0,1) | C. | (-1,1) | D. | (0,1) |
11.下列说法正确的是( )
| A. | 0∉N | B. | $\sqrt{2}$∈Q | C. | π∉R | D. | $\sqrt{4}$∈Z |
17.已知x0(x0>1)是函数f(x)=lnx-$\frac{1}{x-1}$的一个零点,若a∈(1,x0),b∈(x0,+∞),则( )
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)<0,f(b)>0 | D. | f(a)>0,f(b)<0 |
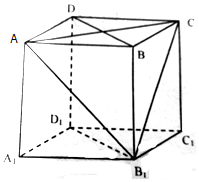 在棱长为2的正方体中,
在棱长为2的正方体中,