题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}4\;|{\;{{log}_2}x\;}|\;\;\;\;\;0<x<2\\ \frac{1}{2}{x^2}-5x+12\;\;\;\;\;x≥2\end{array}$,若存在实数a,b,c,d满足f(a)=f(b)=f(c)=f(d),若d>c>b>a>0,则abc(d-4)的取值范围是( )| A. | (8,9) | B. | (8,9] | C. | (12,32) | D. | [12,32) |
分析 根据图象可判断:$\frac{1}{2}$<a<1,1<b<2,2<c<4,6<d<8,推出ab的值,利用二次函数的值域,求解表达式的范围即可.
解答 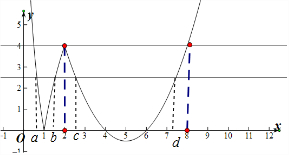 解:若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0
解:若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0
根据图象可判断:$\frac{1}{2}$<a<1,1<b<2,2<c<4,6<d<8,
由二次函数的对称性可知c+d=10.
∵f(a)=f(b),可得:-4log2a=4log2b,
可得ab=1.
abc(d-4)=c(d-4)=c(6-c)=6c-c2=9-(c-3)2,
∵2<c<4,∴c-3∈(-1,1),(c-3)2∈[0,1)
∴9-(c-3)2∈(8,9].
故选:B.
点评 本题综合考查了函数图象的运用,求解两个图象的交点问题,运用动的观点解决,理解好题意是解题关键.

练习册系列答案
相关题目
17.在三棱锥P-ABC中,AB⊥BC,AB=BC=$\sqrt{2}$,PA=PC=2,AC中点为M,cos∠PMB=$\frac{{\sqrt{3}}}{3}$,则此三棱锥的外接球的表面积为( )
| A. | $\frac{3π}{2}$ | B. | 2π | C. | 6π | D. | $\sqrt{6}$π |
15.已知 f(x)=$\frac{a-{2}^{x}}{1+{2}^{x}}$(a∈R)是奇函数,且实数k满足f(2k-1)<$\frac{1}{3}$,则k的取值范围是( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
2.已知sin(α+$\frac{π}{3}$)+sinα=-$\frac{4\sqrt{3}}{5}$.-$\frac{π}{2}$<α<0,则sin(-α+$\frac{5π}{6}$)等于( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
16.设a=log${\;}_{\frac{1}{2}}$3,b=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$,c=2${\;}^{\frac{1}{3}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c? |
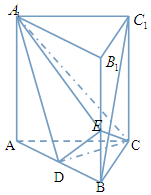 如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.