题目内容
8.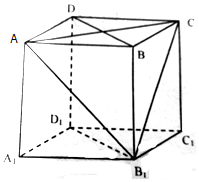 在棱长为2的正方体中,
在棱长为2的正方体中,(1)求异面直线BD与B1C所成的角
(2)求证:平面ACB1⊥平面B1D1DB.
分析 (1)连接B1D1,CD1,由B1D1∥BD,可得∠CB1D1为异面直线BD与B1C所成的角(或补角),运用等边三角形的定义,即可得到所求角;
(2)设AC和BD相交于O,连接OB1,由正方形对角线垂直和等边三角形的性质,可得AC⊥平面B1D1DB,再由面面垂直的判定定理,即可得证.
解答 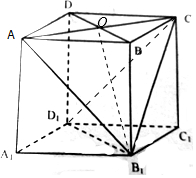 解:(1)连接B1D1,CD1,
解:(1)连接B1D1,CD1,
可得△C1BD1为等边三角形,
由B1D1∥BD,
可得∠CB1D1为异面直线BD与B1C所成的角(或补角),
由∠CB1D1=60°,
可得异面直线BD与B1C所成的角为60°;
(2)证明:设AC和BD相交于O,
连接OB1,
由正方形ABCD可知AC⊥BD,
△ACB1为等边三角形,O为AC的中点,
可得AC⊥OB1,
BD∩OB1=O,BD?平面B1D1DB,OB1?平面B1D1DB,
即有AC⊥平面B1D1DB,
又AC?平面ACB1,
则平面ACB1⊥平面B1D1DB.
点评 本题考查空间异面直线所成角的求法,面面垂直的判定,注意运用定义法和线面垂直的判定定理,考查推理和运算能力,属于中档题.

练习册系列答案
相关题目
16.设a=log${\;}_{\frac{1}{2}}$3,b=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$,c=2${\;}^{\frac{1}{3}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c? |
3.已知2a>2b>1,则下列不等关系式中一定正确的是( )
| A. | sinα>sinb | B. | log2a<log2b | C. | a3<b3 | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
9.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为$\frac{4}{3}$,则球O的表面积为( )
| A. | $\frac{32}{3}π$ | B. | 16π | C. | 144π | D. | 288π |
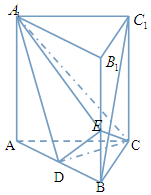 如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.