题目内容
11.已知圆B:(x-1)2+(y-1)2=2,过原点O作两条不同的直线l1,l2与圆B分别交于P,Q.(1)过圆心B作BA⊥OP,BC⊥OQ,垂足分别为点A,C,求过四点O,A,B,C的圆E的方程,并判断圆B与圆E的位置关系;
(2)若l1与l2的倾斜角互补,试用l1的倾斜角α表示△OPQ的面积,并求其最大值.
分析 (1)求出圆心坐标与半径,可得圆E的方程,即可得出结论;
(2)求出直线与圆相交的弦长,可得面积,利用三角函数知识得出结论.
解答 解:(1)过四点O,A,B,C的圆E的方程是以OB为直径的圆,圆E的圆心为($\frac{1}{2}$,$\frac{1}{2}$),半径为$\frac{\sqrt{2}}{2}$,
∴圆E的方程为:(x-$\frac{1}{2}$)2+(y-$\frac{1}{2}$)2=$\frac{1}{2}$.
∵圆心距=$\sqrt{(1-\frac{1}{2})^{2}+(1-\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$=$\sqrt{2}-\frac{\sqrt{2}}{2}$,
∴圆B与圆E相内切;
(2)设l1的方程为y=xtanα,圆心B(1,1)到直线l1的距离d=$\frac{|tanα-1|}{\sqrt{ta{n}^{2}α+1}}$,
直线l1与圆相交的弦长m=$\frac{2|tanα+1|}{\sqrt{ta{n}^{2}α+1}}$,
以-tanα代替tanα,可得直线l2与圆相交的弦长n=2$\frac{|tanα-1|}{\sqrt{ta{n}^{2}α+1}}$,
∴S△OPQ=$\frac{1}{2}mn|sin2α|$=2|$\frac{ta{n}^{2}α-1}{ta{n}^{2}α+1}$||sin2α|=|sin4α|≤1,
当且仅当α=$\frac{π}{8}$,$\frac{3π}{8}$,$\frac{5π}{8}$,$\frac{7π}{8}$时等号成立,故最大值为1.
点评 本题考查直线方程,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
2.已知抛物线C:y2=2px(p>0)的焦点为F,点D(2,y0)在抛物线C上,且|DF|=3,直线y=x-1与抛物线C交于A,B两点,O为坐标原点.
(1)求抛物线C的方程;
(2)求△OAB的面积.
(1)求抛物线C的方程;
(2)求△OAB的面积.
16.已知角θ的始边与x轴的非负半轴重合,终边过点M(-3,4),则cos2θ的值为( )
| A. | $-\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{24}{25}$ | D. | $\frac{24}{25}$ |
3.下列命题中真命题的个数是( )
①“a>b”是“a2>b2”的充要条件;
②“a>b”是“a3>b3”的充要条件;
③“a>b”是“|a|>|b|”的充分条件;
④“a>b”是“ac2≤bc2”的必要条件.
①“a>b”是“a2>b2”的充要条件;
②“a>b”是“a3>b3”的充要条件;
③“a>b”是“|a|>|b|”的充分条件;
④“a>b”是“ac2≤bc2”的必要条件.
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
20.《数学统综》有如下记载:“有凹线,取三数,小小大,存三角”.意思是说“在凹(或凸)函数(函数值为正)图象上取三个点,如果在这三点的纵坐标中两个较小数之和大于最大的数,则存在将这三点的纵坐标值作为三边长的三角形”.现已知凹函数f(x)=x2-2x+2,在$[\frac{1}{3},{m^2}-m+2]$上任取三个不同的点(a,f(a)),(b,f(b)),(c,f(c)),均存在以f(a),f(b),f(c)为三边长的三角形,则实数m的取值范围为( )
| A. | [0,1] | B. | $[0,\frac{{\sqrt{2}}}{2})$ | C. | $(0,\frac{{\sqrt{2}}}{2}]$ | D. | $[\frac{{\sqrt{2}}}{2},\sqrt{2}]$ |
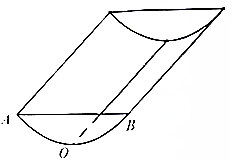 某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.
某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.