题目内容
10.下列说法正确的是( )| A. | 命题“若x2=1,则x=1的否命题为:“若x2=1,则x≠1” | |
| B. | “m=1”是“直线x-my=0和直线x+my=0互相垂直”的充要条件 | |
| C. | 命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“已知A,B为一个三角形两内角,若A=B,则sinA=sinB”的否命题为真命题 |
分析 写出命题的否命题判断A;由两直线垂直与系数的关系求得m判断B;写出特称命题的否定判断C;由充分必要条件的判定方法判断D.
解答 解:命题“若x2=1,则x=1的否命题为:“若x2≠1,则x≠1”,故A错误;
由1×1-m2=0,得m=±1,
∴“m=1”是“直线x-my=0和直线x+my=0互相垂直”的充分不必要条件,故B错误;
命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1≥0”,故C错误;
由三角形中,A=B?a=b?sinA=sinB,得:
命题“已知A,B为一个三角形两内角,若A=B,则sinA=sinB”的否命题为真命题,故D正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了命题的否定与否命题,考查充分必要条件的判定方法,属中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
5.下列说法中正确的是( )
| A. | 命题“?x∈R.ex>0”的否定是“?x∈R,ex>0” | |
| B. | 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题是真命题 | |
| C. | “x2+2x≥ax在x∈[1,2]上恒成立”?“对于x∈[1,2]有(x2+2x)min≥(ax)max” | |
| D. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 |
19.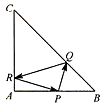 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
20.下列说法中正确的是( )
| A. | 经过不同的三点有且只有一个平面 | |
| B. | 没有公共点的两条直线一定平行 | |
| C. | 垂直于同一平面的两直线是平行直线 | |
| D. | 垂直于同一平面的两平面是平行平面 |