题目内容
5.下列说法中正确的是( )| A. | 命题“?x∈R.ex>0”的否定是“?x∈R,ex>0” | |
| B. | 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题是真命题 | |
| C. | “x2+2x≥ax在x∈[1,2]上恒成立”?“对于x∈[1,2]有(x2+2x)min≥(ax)max” | |
| D. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 |
分析 利用命题的否定判断A的正误;逆命题的真假判断B的正误;恒成立问题判断C的正误;直接判断逆否命题的真假推出D的正误;
解答 解:对于A,命题“?x∈R.ex>0”的否定是“?x∈R,ex>0”,不满足命题的否定形式,所以不正确;
对于B,命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题是假命题,因为a=0时,也只有一个零点,所以B不正确;
对于C,“x2+2x≥ax在x∈[1,2]上恒成立”?“对于x∈[1,2]有(x2+2x)min≥(ax)max”,表示有,而是恒有(x2+2x)min≥(ax)max,所以C不正确;
对于D,命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题,它的逆否命题是:x=2且y=1则x+y=3,显然,逆否命题是真命题,所以D正确.
故选:D.
点评 本题考查命题的真假的判断与应用,注意基本知识的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(-$\frac{π}{6}$)的值为( )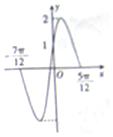

| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
20.已知tanα=-$\frac{3}{4}$,tan(π-β)=$\frac{1}{2}$,则tan(α-β)的值为( )
| A. | -$\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | -$\frac{11}{2}$ |
10.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1的否命题为:“若x2=1,则x≠1” | |
| B. | “m=1”是“直线x-my=0和直线x+my=0互相垂直”的充要条件 | |
| C. | 命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“已知A,B为一个三角形两内角,若A=B,则sinA=sinB”的否命题为真命题 |
14.已知菱形ABCD的边长为4,∠ABC=120°,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( )
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{{\sqrt{3}π}}{24}$ | D. | $1-\frac{{\sqrt{3}π}}{24}$ |