题目内容
15.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(2,0),点P(1,-$\frac{\sqrt{15}}{3}$)在椭圆C上.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)是否存在斜率为-1直线l与椭圆C相交于M,N两点,使得|F1M|=|F1N|(F1为椭圆的左焦点)?若存在,求出直线l的方程;若不存在,说明理由.
分析 (Ⅰ)由椭圆的右焦点为F2(2,0),点P(1,-$\frac{\sqrt{15}}{3}$)在椭圆C上,列出方程组求出a,b,由此能求出椭圆C的标准方程.
(Ⅱ)假设存在斜率为-1直线l:y=-x+m与椭圆C相交于M(x1,y1),N(x2,y2)两点,使得|F1M|=|F1N|,联立$\left\{\begin{array}{l}{y=-x+m}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得:4x2-6mx+3m2-6=0,由此利用根的判别式、韦达定理、两点间距离公式、直线斜率公式,结合已知条件推导出不存在斜率为-1直线l与椭圆C相交于M,N两点,使得|F1M|=|F1N|.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(2,0),点P(1,-$\frac{\sqrt{15}}{3}$)在椭圆C上,
∴$\left\{\begin{array}{l}{c=2}\\{\frac{1}{{a}^{2}}+\frac{15}{9{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=$\sqrt{6}$,b=$\sqrt{2}$,
∴椭圆C的标准方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$.
(Ⅱ)不存在斜率为-1直线l与椭圆C相交于M,N两点,使得|F1M|=|F1N|.
理由如下:
假设存在斜率为-1直线l:y=-x+m与椭圆C相交于M(x1,y1),N(x2,y2)两点,使得|F1M|=|F1N|,
联立$\left\{\begin{array}{l}{y=-x+m}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消除y,得:4x2-6mx+3m2-6=0,
△=36m2-16(3m2-6)>0,解得-2$\sqrt{2}<m<2\sqrt{2}$,(*)
${x}_{1}+{x}_{2}=\frac{3m}{2},{x}_{1}{x}_{2}=\frac{3{m}^{2}-6}{4}$,${y}_{1}+{y}_{2}=2m-({x}_{1}+{x}_{2})=2m-\frac{3m}{2}=\frac{m}{2}$,
∵M(x1,y1),N(x2,y2),F1(-2,0),|F1M|=|F1N|,
∴$\sqrt{({{x}_{1}}^{\;}+2)^{2}+{{y}_{1}}^{2}}=\sqrt{({{x}_{2}+2)}^{2}+{{y}_{2}}^{2}}$,
整理,得(x1+x2+4)(x1-x2)+(y1+y2)(y1-y2)=0,
∴$\frac{3m+8}{2}({x}_{1}-{x}_{2})+\frac{m}{2}({y}_{1}-{y}_{2})=0$,
∴直线l:y=-x+m的斜率:-1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=\frac{\frac{3m+8}{2}}{-\frac{m}{2}}$=-$\frac{3m+8}{m}$,
解得m=-4,不满足(*)式,
∴不存在斜率为-1直线l与椭圆C相交于M,N两点,使得|F1M|=|F1N|.
点评 本题考查椭圆方程的求法,考查满足条件的直线是否存在的判断与求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、两点间距离公式、直线斜率公式的合理运用.

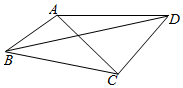 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.