题目内容
10.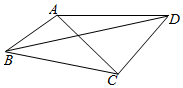 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.
分析 设∠ABC=α,∠ACB=β,求出AC,sinβ,利用余弦定理,即可求出对角线BD的最大值.
解答 解:设∠ABC=α,∠ACB=β,则AC2=4-2$\sqrt{3}$cosα,
由正弦定理可得sinβ=$\frac{sinα}{\sqrt{4-2\sqrt{3}cosα}}$,
∴BD2=3+4-2$\sqrt{3}$cosα-2×$\sqrt{3}$×$\sqrt{4-2\sqrt{3}cosα}$×cos(90°+β)=7-2$\sqrt{3}$cosα+2$\sqrt{3}$sinα=7+2$\sqrt{6}$sin(α-45°),
∴α=135°时,BD取得最大值$\sqrt{6}$+1.
故答案为:$\sqrt{6}$+1.
点评 本题考查余弦定理、正弦定理的运用,考查辅助角公式的运用,考查学生的计算能力,有难度.

练习册系列答案
相关题目
20.设i为虚数单位,则复数3-i的虚部是( )
| A. | 3 | B. | -i | C. | 1 | D. | -1 |
1.已知x,y满足不等式$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y≤25\\ x≥1\end{array}\right.$,则函数z=2x+y取得最大值是( )
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
18.已知在某个回归分析中有甲、乙、丙三个模型,其R2的值依次为0.64、0.80和0.98,则下列说法正确的是( )
| A. | 甲模型拟合效果最好 | B. | 乙模型拟合效果最好 | ||
| C. | 丙模型拟合效果最好 | D. | 拟合效果与R2的值无关 |
19.甲盒子里装有分别标有数字1,2,4,7的4张卡片,乙盒子里装有分别标有数字1,4的2张卡片,若从两个盒子中各随机地摸取出1张卡片,则2张卡片上的数字之积为奇数的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
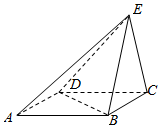 如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.