题目内容
6.一个几何体的某一方向的视图是圆,则它不可能是( )| A. | 球体 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
分析 由三视图的定义对四个选项依次验证,检验其是否符合题目要求,即可选取正确选项.
解答 解:对于选项A,球的三个视图都是圆,故此几何体可以是球,A不是正确选项;
对于选项B,圆柱的俯视图是圆,故B不是正确选项;
对于选项C,圆锥的俯视图是圆,故C不是正确选项;
对于选项D,长方体的三个视图都是矩形,其俯视图不可能是圆,故D为正确选项
故选D.
点评 本题考点是简单空间图形的三视图,考查根据作三视图的规则来作出三个视图的能力,三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于如表中:
(1)求椭圆C1和抛物线C2的标准方程.
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,
①试证:直线PA,PF,PB的斜率成等差数列.
②若点P在X轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
| x | -2 | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{2}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,
①试证:直线PA,PF,PB的斜率成等差数列.
②若点P在X轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
18.定积分${∫}_{0}^{π}$|sinx-cosx|dx的值是( )
| A. | 2+$\sqrt{2}$ | B. | 2-$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
13.已知三次函数f(x)=ax3+x-b(a>0)在区间(0,1]内有零点,且f′(1)≤4,则f(-2)的取值范围是( )
| A. | (-10,-6) | B. | [-12,-2) | C. | [-12,-6) | D. | [-12,-10) |
 ,则输出的
,则输出的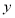 等于( )
等于( )
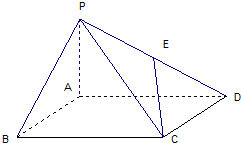
 如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形
如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形 如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.