题目内容
11. 如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.(1)求证:平面PCD⊥平面PAC;
(2)求直线PB与平面PCD所成角的大小.
分析 (1)利用余弦定理求出AC,根据勾股定理得出AB⊥AC,即CD⊥AC,由PA⊥平面ABCDE得出CD⊥PA,故CD⊥平面PAC,从而得出平面PAC⊥平面PCD;
(2)做AM⊥PC即可证明AM⊥平面PCD,又AB∥CD,故B到平面PCD的距离h=AM,求出AM,BP的值即可得出直线PB与平面PCD所成角的正弦值.
解答 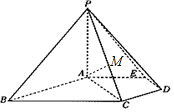 (1)证明:在△ABC中,∵∠ABC=45°,BC=4,AB=2$\sqrt{2}$,
(1)证明:在△ABC中,∵∠ABC=45°,BC=4,AB=2$\sqrt{2}$,
∴AC2=AB2+BC2-2AB•BC•cos45°=8,
∴AC=2$\sqrt{2}$,∴BC2=AB2+AC2,
∴BA⊥AC.
又PA⊥平面ABCDE,AB∥CD,CD?平面ABCDE,
∴CD⊥PA,CD⊥AC,
又PA?平面PAC,AC?平面PAC,PA∩AC=A,
∴CD⊥平面PAC,又CD?平面PCD,
∴平面PCD⊥平面PAC.
(2)∵AB=AP=AC=2$\sqrt{2}$,
∴PB=PC=$\sqrt{2}$AB=4,
过A做AM⊥PC,则AM=$\frac{AP•AC}{PC}$=2,
∵平面APC⊥平面PCD,平面APC∩平面PCD=PC,AM⊥PC,AM?平面APC,
∴AM⊥平面PCD,
即A到平面PCD的距离为AM=2,
∵AB∥CD,
∴B到平面PCD的距离h=AM=2,
设直线PB与平面PCD所成角为θ,
∴sinθ=$\frac{h}{BP}$=$\frac{1}{2}$,∴θ=30°.
点评 本题考查了面面垂直的判定,线面角的计算,也可利用空间向量求出,属于中档题.

练习册系列答案
相关题目
6.一个几何体的某一方向的视图是圆,则它不可能是( )
| A. | 球体 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
3.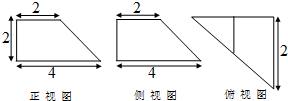 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )| A. | 6+12$\sqrt{2}$ | B. | 16+12$\sqrt{2}$ | C. | 6+12$\sqrt{3}$ | D. | 16+12$\sqrt{3}$ |
19.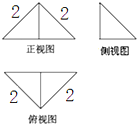 把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
 把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )| A. | 2$\sqrt{3}$+4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 2$\sqrt{3}$+2 |
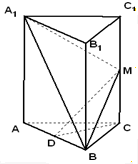 在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM
在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM