题目内容
15. 如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形
如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.
(Ⅰ)求证:CB⊥面PEB
(Ⅱ) 已知$\overrightarrow{PF}=λ\overrightarrow{PC}({λ∈R})$,且PA∥面BEF,求λ的值.
分析 (Ⅰ)先求出$PE=\sqrt{3}$,从而PE⊥AD,再由面面垂直的性质定理,以及线面垂直的判定定理,即可证得CB⊥面PEB;
(Ⅱ)连接AC交BE于点M,连接FM,运用线面平行的性质定理,得到PA∥FM,再由平行线分线段成比例,得到λ的值.
解答 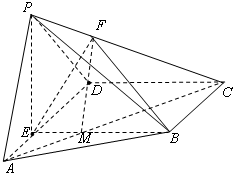 (Ⅰ)证明:∵AP=2,AE=1,∠PAD=60°,
(Ⅰ)证明:∵AP=2,AE=1,∠PAD=60°,
∴$PE=\sqrt{3}$,
∴PE⊥AD.
又面PAD⊥面ABCD,且面PAD∩面ABCD=AD,PE⊥面ABCD,
∴PE⊥CB,
又∴BE⊥CB,且PE∩BE=E,
∴CB⊥面PEB.
(Ⅱ)解:连接AC交BE于点M,连接FM.
∵PA∥面BEF,
∴FM∥AP,
∵EM∥CD,
∴$\frac{AM}{MC}=\frac{AE}{ED}=\frac{1}{2}$
∵FM∥AP,
∴$\frac{PF}{FC}=\frac{AM}{MC}=\frac{1}{2}$,
∴$λ=\frac{1}{3}$.
点评 本题考查线面平行的性质定理和线面垂直的判定和性质定理,面面垂直的性质定理,同时考查等积法求点到平面的距离,平行线分线段成比例等,属于中档题.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
7.国务院总理李克强在2015年4月14日的经济形势座谈会上就“手机流量资费和网速”问题做出重要指示,工信部回应,将加大今年宽带专项行动中“加快4G建设”、“大幅提升网速”等重点工作的推进力度,为此某移动部门对部分4G手机用户每日使用流量(单位:M)进行统计,得到如下记录:
将手机日使用流量统计到各组的频率视为概率,并假设每天手机日使用流量相互独立.
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
| 流量(x) | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
10.设向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}$|=1,$\overrightarrow a•\overrightarrow b=m$,则$|{\overrightarrow a+t\overrightarrow b}|({t∈R})$的最小值为( )
| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
6.一个几何体的某一方向的视图是圆,则它不可能是( )
| A. | 球体 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
3.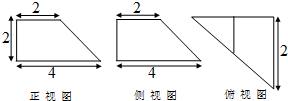 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )| A. | 6+12$\sqrt{2}$ | B. | 16+12$\sqrt{2}$ | C. | 6+12$\sqrt{3}$ | D. | 16+12$\sqrt{3}$ |
2.正方形ABCD沿对角线BD将△ABD折起,使A点至P点,连PC.已知二面角P-BD-C的大小为θ,则下列结论错误的是( )
| A. | 若θ=90°,则直线PB与平面BCD所成角大小为45° | |
| B. | 若直线PB与平面BCD所成角大小为45°,则θ=90° | |
| C. | 若θ=60°,则直线BD与PC所成角大小为90° | |
| D. | 若直线BD与PC所成角大小为90°,则θ=60° |
 为锐角,且
为锐角,且 ,则
,则 .
.