题目内容
13.已知三次函数f(x)=ax3+x-b(a>0)在区间(0,1]内有零点,且f′(1)≤4,则f(-2)的取值范围是( )| A. | (-10,-6) | B. | [-12,-2) | C. | [-12,-6) | D. | [-12,-10) |
分析 先求导,判断函数f(x)在(0,1]上单调递增,则f(0)<0且f(1)≥0,以及根据f′(1)≤4,求出a,b的范围,代计算即可.
解答 解:f(x)=ax3+x-b(a>0),
∴f′(x)=3ax2+1>0,在(0,1]内恒成立,
∴f(x)在(0,1]上单调递增,
∵f′(1)≤4,
∴3a+1≤4,
∴a≤1,
∴0<a≤1
∵函数f(x)=ax3+x-b(a>0)在区间(0,1]内有零点,
∴f(0)<0且f(1)≥0,
∴-b<0,且a+1-b≥0,
∴0<b≤2,
∴-2≤-b<0,
∴f(-2)=-8a-2-b,
∵0<a≤1,
∴-8≤-8a<0,
∴-10≤-8a-2<-2,
∴-12≤-8a-2-b<-2
故-12≤f(-2)<-2,
故选:B
点评 本题考查了导数和函数的单调性和关系,以及零点存在定理和不等式的基本性质,属于中档题.

练习册系列答案
相关题目
6.一个几何体的某一方向的视图是圆,则它不可能是( )
| A. | 球体 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
2.正方形ABCD沿对角线BD将△ABD折起,使A点至P点,连PC.已知二面角P-BD-C的大小为θ,则下列结论错误的是( )
| A. | 若θ=90°,则直线PB与平面BCD所成角大小为45° | |
| B. | 若直线PB与平面BCD所成角大小为45°,则θ=90° | |
| C. | 若θ=60°,则直线BD与PC所成角大小为90° | |
| D. | 若直线BD与PC所成角大小为90°,则θ=60° |
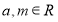 ,
,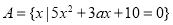 ,
,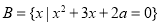 ,
,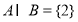 ,
,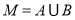 .
.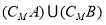 ;
;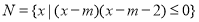 ,且
,且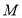 中有且仅有2个元素属于
中有且仅有2个元素属于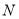 ,求
,求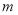 的取值范围.
的取值范围.
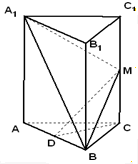 在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM
在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM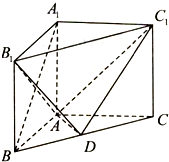 如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=AC=AA1=2.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=AC=AA1=2.