题目内容
1.已知椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于如表中:| x | -2 | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{2}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,
①试证:直线PA,PF,PB的斜率成等差数列.
②若点P在X轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
分析 (1)设抛物线方程为y2=mx,代入4个点,可得m,检验可知m=1成立,再将其余两个点代入椭圆方程,解得a,b,进而得到椭圆方程;
(2)①讨论当直线AB的斜率为0时,设P(4,y0),可得结论;当直线AB的斜率不为0时,
设AB:x=ty+2,代入x2+2y2=8,消去x,运用韦达定理和直线的斜率公式,化简整理,再结合向量的坐标表示,向量模的平方即为向量的平方,结合二次函数最值求法,可得t的值,进而得到所求直线方程.
解答 解:(1)设抛物线方程为y2=mx,分别将四个点代入解得m=-1,m=1,m=$\frac{\sqrt{6}}{6}$,m=1,
故抛物线方程为y2=x;即点(2,-$\sqrt{2}$)和(9,3)在抛物线上.
因此(-2,$\sqrt{2}$),($\sqrt{6}$,-1)两个点为椭圆C1上两点,
设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
将上述两个点坐标代入$\frac{4}{{a}^{2}}$+$\frac{2}{{b}^{2}}$=1,$\frac{6}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,
解得:a2=8,b2=4,
故椭圆方程为:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1. (4分)
(2)①证明:当直线AB的斜率为0时,
设P(4,y0),则kPA+kPB=y0=2kPF,直线PA,PF,PB的斜率成等差数列; (5分)
当直线AB的斜率不为0时,
设AB:x=ty+2,代入x2+2y2=8,消去x,可得(2+t2)y2+4ty-4=0,
设A(x1,y1),B(x2,y2),则y1+y2=-$\frac{4t}{2+{t}^{2}}$,y1y2=-$\frac{4}{2+{t}^{2}}$,
则有:kPA+kPB=$\frac{{y}_{0}-{y}_{1}}{2-t{y}_{1}}$+$\frac{{y}_{0}-{y}_{2}}{2-t{y}_{2}}$=$\frac{4{y}_{0}-(2+t{y}_{0})({y}_{1}+{y}_{2})+2t{y}_{1}{y}_{2}}{4-2t({y}_{1}+{y}_{2})+{t}^{2}{y}_{1}{y}_{2}}$=y0=2kPF,
则直线PA,PF,PB的斜率成等差数列 (7分)
$\overrightarrow{②}$因为$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],所以$\frac{{y}_{1}}{{y}_{2}}$=λ,且λ<0.
又y1+y2=-$\frac{4t}{2+{t}^{2}}$,y1y2=-$\frac{4}{2+{t}^{2}}$,
则$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=$\frac{{{y}_{1}}^{2}+2{y}_{1}{y}_{2}+{{y}_{2}}^{2}}{{y}_{1}{y}_{2}}$=λ+$\frac{1}{λ}$+2,
又$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=-$\frac{4{t}^{2}}{2+{t}^{2}}$,
即λ+$\frac{1}{λ}$+2=-$\frac{4{t}^{2}}{2+{t}^{2}}$,
由λ∈[-2,-1],得λ+$\frac{1}{λ}$∈[-$\frac{5}{2}$,-2],即t2∈[0,$\frac{2}{7}$],
因为P(4,0),$\overrightarrow{PA}$=(x1-4,y1),$\overrightarrow{PB}$=(x2-4,y2),
所以$\overrightarrow{PA}$+$\overrightarrow{PB}$=(x1+x2-8,y1+y2)=(ty1+ty2-4,y1+y2),
故|$\overrightarrow{PA}$+$\overrightarrow{PB}$|2=(ty1+ty2-4)2+(y1+y2)2=(-$\frac{4{t}^{2}}{2+{t}^{2}}$-4)2+(-$\frac{4t}{2+{t}^{2}}$)2=$\frac{(8{t}^{2}+8)^{2}+16{t}^{2}}{(2+{t}^{2})^{2}}$,
令m=2+t2(m∈[2,$\frac{16}{7}$]),则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|2=$\frac{(8m-8)^{2}+16(m-2)}{{m}^{2}}$=64-$\frac{112}{m}$+$\frac{32}{{m}^{2}}$
=2($\frac{4}{m}$-7)2-34=32($\frac{1}{m}$-$\frac{7}{4}$)2-34,
当$\frac{1}{m}$=$\frac{7}{16}$ 即t2=$\frac{2}{7}$时,|$\overrightarrow{PA}$+$\overrightarrow{PB}$|2的值最大,
此时方程为x=±$\frac{\sqrt{14}}{7}$y+2. (13分)
点评 本题考查椭圆和抛物线方程的求法,注意运用代入法,考查直线和椭圆方程联立,运用韦达定理,以及向量坐标表示,考查化简整理的运算能力,属于难题.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
| A. | 球体 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
 :
: 与直线
与直线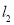 :
: 平行,且
平行,且 与圆
与圆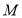 :
: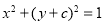 相切,则
相切,则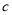 的值为( )
的值为( ) B.
B. C.
C.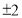 D.
D.
 如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.