题目内容
14.在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AC=2AB,M是CC1的中点,N是棱AC上的点,且$\overrightarrow{{A_1}N}⊥\overrightarrow{BM},|{\overrightarrow{{A_1}N}}|=2\sqrt{5}$,求三棱锥A1-ABN的体积.分析 以A为原点建立坐标系,设AB=a,AN=b,求出$\overrightarrow{{A}_{1}N}$和$\overrightarrow{BM}$的坐标,列出方程组求出a,b的值,代入棱锥的体积公式计算.
解答  解:以A为原点,以AC,AB,AA1所在直线为坐标轴建立空间直角坐标系A-xyz,
解:以A为原点,以AC,AB,AA1所在直线为坐标轴建立空间直角坐标系A-xyz,
设AB=a,AN=b,则A1(0,0,2a),B(0,a,0),N(b,0,0),M(2a,0,a),
∴$\overrightarrow{{A}_{1}N}$=(b,0,-2a),$\overrightarrow{BM}$=(2a,-a,a),
∵$\overrightarrow{{A_1}N}⊥\overrightarrow{BM},|{\overrightarrow{{A_1}N}}|=2\sqrt{5}$,
∴$\left\{\begin{array}{l}{2ab-2{a}^{2}=0}\\{{b}^{2}+4{a}^{2}=20}\end{array}\right.$,解得a=b=2,
∴V${\;}_{{A}_{1}-ABN}$=$\frac{1}{3}{S}_{△ABN}•A{A}_{1}$=$\frac{1}{3}×\frac{1}{2}×2×2×4$=$\frac{8}{3}$.
点评 本题考查了棱锥的体积计算,空间向量在立体几何中的应用,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
7.国务院总理李克强在2015年4月14日的经济形势座谈会上就“手机流量资费和网速”问题做出重要指示,工信部回应,将加大今年宽带专项行动中“加快4G建设”、“大幅提升网速”等重点工作的推进力度,为此某移动部门对部分4G手机用户每日使用流量(单位:M)进行统计,得到如下记录:
将手机日使用流量统计到各组的频率视为概率,并假设每天手机日使用流量相互独立.
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
| 流量(x) | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
6.一个几何体的某一方向的视图是圆,则它不可能是( )
| A. | 球体 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
3.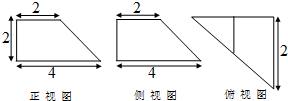 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )| A. | 6+12$\sqrt{2}$ | B. | 16+12$\sqrt{2}$ | C. | 6+12$\sqrt{3}$ | D. | 16+12$\sqrt{3}$ |
19.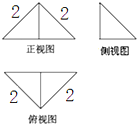 把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
 把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )| A. | 2$\sqrt{3}$+4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 2$\sqrt{3}$+2 |
2.正方形ABCD沿对角线BD将△ABD折起,使A点至P点,连PC.已知二面角P-BD-C的大小为θ,则下列结论错误的是( )
| A. | 若θ=90°,则直线PB与平面BCD所成角大小为45° | |
| B. | 若直线PB与平面BCD所成角大小为45°,则θ=90° | |
| C. | 若θ=60°,则直线BD与PC所成角大小为90° | |
| D. | 若直线BD与PC所成角大小为90°,则θ=60° |
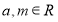 ,
,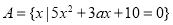 ,
,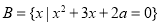 ,
,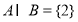 ,
,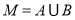 .
.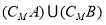 ;
;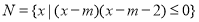 ,且
,且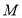 中有且仅有2个元素属于
中有且仅有2个元素属于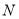 ,求
,求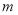 的取值范围.
的取值范围.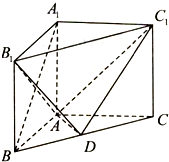 如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=AC=AA1=2.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=AC=AA1=2.