题目内容
18.如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点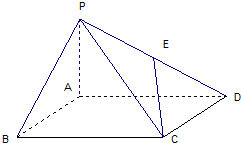
(1)求异面直线PA与CE所成角的大小;
(2)求三棱锥A-CDE的体积.
分析 (1)过E作EF⊥AD交AD于F,则∠CEF是异面直线PA与CE的夹角,由此能求出异面直线PA与CE所成角的大小.
(2)三棱锥A-CDE的体积VA-CDE=VEACD,由此能求出三棱锥A-CDE的体积.
解答 (本题满分12分)本题共有2个小题,第1小题满分(5分),第2小题满分(7分).
解:(1)过E作EF⊥AD交AD于F,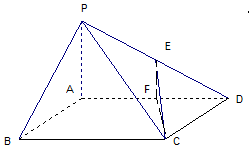
则∠CEF是异面直线PA与CE的夹角
连结CF,在Rt△CEF中,
∵EF=$\frac{1}{2}$,CF=$\sqrt{2}$,∴tan∠CEF=$\frac{CF}{EF}$=2$\sqrt{2}$.
∴∠CEF=arctan2$\sqrt{2}$.
∴异面直线PA与CE所成角的大小为arctan2$\sqrt{2}$.
(2)三棱锥A-CDE的体积:
VA-CDE=VEACD=$\frac{1}{3}×(\frac{1}{2}×1×2)×\frac{1}{2}=\frac{1}{6}$.
点评 本题考查异面直线所居角的大小的求法,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.国务院总理李克强在2015年4月14日的经济形势座谈会上就“手机流量资费和网速”问题做出重要指示,工信部回应,将加大今年宽带专项行动中“加快4G建设”、“大幅提升网速”等重点工作的推进力度,为此某移动部门对部分4G手机用户每日使用流量(单位:M)进行统计,得到如下记录:
将手机日使用流量统计到各组的频率视为概率,并假设每天手机日使用流量相互独立.
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
| 流量(x) | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
10.设向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}$|=1,$\overrightarrow a•\overrightarrow b=m$,则$|{\overrightarrow a+t\overrightarrow b}|({t∈R})$的最小值为( )
| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
6.一个几何体的某一方向的视图是圆,则它不可能是( )
| A. | 球体 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
 ,其中
,其中 ,若
,若 的值域是
的值域是 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
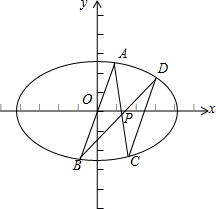 如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点A($\frac{1}{3}$,$\frac{2}{3}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP、BP与椭圆E的另一交点分别为C,D.
如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点A($\frac{1}{3}$,$\frac{2}{3}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP、BP与椭圆E的另一交点分别为C,D. 如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2. ,
,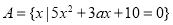 ,
,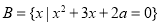 ,
,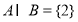 ,
,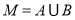 .
.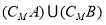 ;
;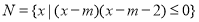 ,且
,且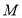 中有且仅有2个元素属于
中有且仅有2个元素属于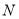 ,求
,求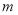 的取值范围.
的取值范围.