题目内容
已知{an}为等差数列，其公差为-2，且a7是a3与a9的等比中项，Sn为{an}的前n项和，n∈N*，则S10的值为 ．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由题意可得a1的方程，解方程得a1代入等差数列的求和公式可得．
解答：
解：∵{an}为等差数列，其公差d=-2，且a7是a3与a9的等比中项，
∴（a1-12）2=（a1-4）（a1-16），解得a1=20，
∴S10=10a1+
d=110
故答案为：110
∴（a1-12）2=（a1-4）（a1-16），解得a1=20，
∴S10=10a1+
| 10×9 |
| 2 |
故答案为：110
点评：本题考查等差数列的求和公式，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
某家具生产厂需要在一个半径为1的圆形木料中依照图纸方式切割出如图十字图形，其中∠AEF=θ（θ为变量），AB=HG=x，AF=y．如图中所示的对应，其中构成映射的个数为（ ）
| A、3 | B、4 | C、5 | D、6 |
设{an}是公差为正数的等差数列，a1+a2+a3=15，a1a2a3=80，则a6+a7+a8=（ ）
| A、40 | B、50 | C、60 | D、70 |
设全集I={0，1，2，3，4，5}，集合A={0，1，2}，集合B={2，4，5}，则∁IA∪B=（ ）
| A、{4，5} |
| B、{0，1，2，3} |
| C、{2，3，4，5} |
| D、{0，1，2，3，4，5} |
设a=log0.53，b=(
)0.2，c=
，则（ ）
| 1 |
| 3 |
| 3 | 2 |
| A、a＜b＜c |
| B、c＜b＜a |
| C、c＜a＜b |
| D、b＜a＜c |
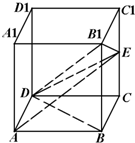在棱长为2的正方体ABCD-A1B1C1D1中，设E是棱CC1的中点．