题目内容
已知|
|=4，|
|=3．
（1）
∥
，求
与
的数量积；
（2）
⊥
，求
与
的数量积；
（3）
与
的夹角为60°时，求
与
的数量积．
| a |
| b |
（1）
| a |
| b |
| a |
| b |
（2）
| a |
| b |
| a |
| b |
（3）
| a |
| b |
| a |
| b |
考点：数量积表示两个向量的夹角,平面向量数量积的运算
专题：平面向量及应用
分析：（1）当
∥
时，
与
的夹角为0°或180°，由数量积的定义可得；
（2）当
⊥
时，
与
的夹角为90°，由数量积的定义可得；
（3）已知
与
的夹角为60°，由数量积的定义可得．
| a |
| b |
| a |
| b |
（2）当
| a |
| b |
| a |
| b |
（3）已知
| a |
| b |
解答：
解：（1）当
∥
时，
与
的夹角为0°或180°
∴
与
的数量积
•
=4×3×1=12，或
•
=4×3×（-1）=-12；
（2）当
⊥
时，
与
的夹角为90°
与
的数量积
•
=4×3×0=0，；
（3）当
与
的夹角为60°时，
与
的数量积
•
=4×3×
=6
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
（2）当
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（3）当
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
点评：本题考查数量积的夹角和数量积的运算，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知平行六面体ABCD-A1B1C1D1中各棱长都有为a，底面ABCD是正方形，顶点A1在平面ABCD上的射影是正方形ABCD的中心O．（1）求证：A1C⊥平面BDD1B1；
（2）求平行六面体的体积．
设集合A={x|x=2k-1，k∈Z}，则（ ）
| A、3∈A | B、3∉A |
| C、3⊆A | D、3?A |
函数f(x)=
的定义域为（ ）
| 1 |
| log3(3x-2) |
A、[
| ||
B、（
| ||
C、[
| ||
D、（
|
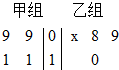以下茎叶图记录了甲、乙两组各四名同学的植树棵树． 乙组记录中有一个数据模糊，无法辨认，在图中以X表示．