题目内容
18.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,若在C上存在一点P,使得PO=$\frac{1}{2}$|F1F2|(O为坐标原点),且直线OP的斜率为$\frac{4}{3}$,则,双曲线C的离心率为$\sqrt{5}$.分析 依题意可知|PO|=$\frac{1}{2}$|F1F2|判断出∠F1PF2=90°,直线OP的斜率为$\frac{4}{3}$,可求出出|PF2|=$\frac{4}{\sqrt{5}}$c,则|F1P|=$\frac{2}{\sqrt{5}}$c,进而利用双曲线定义可用c表示出a,最后可求得双曲线的离心率.
解答 解:∵|PO|=$\frac{1}{2}$|F1F2|,
∴|OF1|=|OF2|=|OP|
∴∠F1PF2=90°,
∵直线OP的斜率为$\frac{4}{3}$,
∴tan∠POF1=$\frac{4}{3}$,
∴cos∠POF1=$\frac{3}{5}$
由余弦定理可得|PF1|2=c2+c2-2c2•$\frac{3}{5}$=$\frac{4}{5}$c2,
即|PF1|=$\frac{2c}{\sqrt{5}}$,
同理可得|PF2|=$\frac{4c}{\sqrt{5}}$,
∴$\frac{4c}{\sqrt{5}}$-$\frac{2c}{\sqrt{5}}$=2a,
∴$\frac{c}{a}$=$\sqrt{5}$
∴e=$\sqrt{5}$.
故答案为:$\sqrt{5}$
点评 本题主要考查了双曲线的简单性质,考查了学生对双曲线定义的理解和灵活运用,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
6.下列函数,是偶函数,且周期为π的是( )
| A. | y=cos2x-sin2x | B. | y=sin2x+cos2x | C. | y=cos2x-sin2x | D. | y=sin2x+cosx |
3.“a=-1”是“直线ax+3y+2=0与直线x+(a-2)y+1=0平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
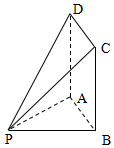 如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.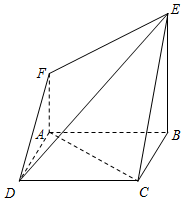 在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.
在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.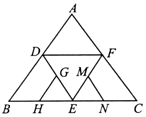 如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论:
如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论: