题目内容
已知向量
=(-3,1),
=(1,-2),
=
+k
(k∈R)
①若向量
与向量2
-
垂直,求实数k的值
②若向量
与向量2
-
共线,求实数k的值
③设向量
与
的夹角为α,
与
的夹角为β,是否存在实数k使α+β=π?求实数k的值,若不存在说明理由?
| a |
| b |
| m |
| a |
| b |
①若向量
| m |
| a |
| b |
②若向量
| m |
| a |
| b |
③设向量
| a |
| m |
| b |
| m |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:①由向量
、
的坐标,求出
与2
-
的坐标,根据向量垂直的坐标表示建立关于k的等式,解之可得满足条件的实数k的值;
②根据向量
与2
-
的坐标,利用向量平行的条件建立关于k的等式,解之可得满足条件的实数k的值;
③设向量
、
、
的起点为O,终点分别为A、B、M,则当点M落在∠AOB的补角∠AOC的平分线上时,满足α+β=π.此时点M到直线OA、OB的距离相等,且M在第二或第四象限内,利用点到直线的距离公式建立关于k的方程,解之可得:存在k=-
,使α+β=π成立.
| a |
| b |
| m |
| a |
| b |
②根据向量
| m |
| a |
| b |
③设向量
| a |
| b |
| m |
| 2 |
解答:
解:∵
=(-3,1),
=(1,-2),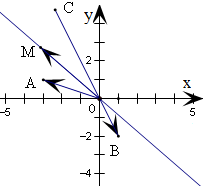
∴
=
+k
=(k-3,-2k+1),2
-
=(-7,4)
①∵向量
与向量2
-
垂直,
∴(k-3)×(-7)+(-2k+1)×4=0,解之得k=
;
②∵向量
与向量2
-
共线,
∴(k-3)×4-(-7)×(-2k+1)=0,解之得k=
;
③设
=
=(-3,1),
=
=(1,-2),
=
=(k-3,-2k+1),
此时∠MOA=α,∠MOB=β,α+β=∠MOA+∠MOB,
设∠AOC是∠AOB的补角,则当M在∠AOC的平分线上时,α+β=∠MOC+∠MOB=π.
直线OA的方程为x+3y=0,直线OB的方程为2x+y=0,点M(k-3,-2k+1)到直线OA、OB的距离相等.
∴
=
,解之得k=±
.
又∵点M(k-3,-2k+1)是第二或第四象限内的点,
∴(k-3)(-2k+1)<0,解得k<
或k>3,由此可得k=
不符合题意,舍去.
综上所述,存在k=-
,使α+β=π成立.
| a |
| b |

∴
| m |
| a |
| b |
| a |
| b |
①∵向量
| m |
| a |
| b |
∴(k-3)×(-7)+(-2k+1)×4=0,解之得k=
| 5 |
| 3 |
②∵向量
| m |
| a |
| b |
∴(k-3)×4-(-7)×(-2k+1)=0,解之得k=
| 19 |
| 10 |
③设
| OA |
| a |
| OB |
| b |
| OM |
| m |
此时∠MOA=α,∠MOB=β,α+β=∠MOA+∠MOB,
设∠AOC是∠AOB的补角,则当M在∠AOC的平分线上时,α+β=∠MOC+∠MOB=π.
直线OA的方程为x+3y=0,直线OB的方程为2x+y=0,点M(k-3,-2k+1)到直线OA、OB的距离相等.
∴
| |k-3+3(-2k+1)| | ||
|
| |2(k-3)-2k+1| | ||
|
| 2 |
又∵点M(k-3,-2k+1)是第二或第四象限内的点,
∴(k-3)(-2k+1)<0,解得k<
| 1 |
| 2 |
| 2 |
综上所述,存在k=-
| 2 |
点评:本题给出向量含有参数k的坐标,探索两个向量平行、垂直的位置关系.着重考查了平面向量的坐标运算、向量平行与垂直的条件、点到直线的距离公式及其应用等知识,属于中档题.

练习册系列答案
相关题目
 如图所示是一个几何体的三视图,则该几何体的体积为( )
如图所示是一个几何体的三视图,则该几何体的体积为( )| A、16+2π | B、8+2π |
| C、16+π | D、8+π |
已知函数f(x)的图象是连续不断的,有如下x,f(x)对应值表:
其中a<c<0<b,则函数f(x)在区间[1,6]上零点至少有( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 10 | 13 | c | 7 | a | b |
| A、2个 | B、3个 | C、4个 | D、5个 |
一个空间几何体的三视图及其相关数据如图所示,则这个空间几何体的表面积是( )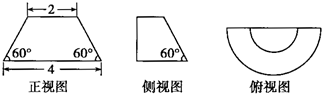

A、
| ||||
B、
| ||||
| C、11π | ||||
D、
|
已知函数f(x)=|x2-6|,若a<b<0,且f(a)=f(b),则a2b的最小值是( )
| A、-16 | B、-12 |
| C、-10 | D、-8 |
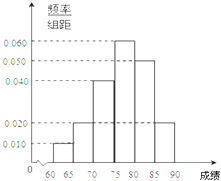 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为