题目内容
已知函数y=sin(ωx+θ)(ω>0,0<θ<π)为偶函数,其图象与直线y=1的两个不同交点的横坐标为x1,x2,若|x1-x2|=kπ,k∈N*,则ω×θ的值为 .
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由题意函数y=sin(ωx+θ)(ω>0,0<θ<π)为偶函数,求出θ,通过|x1-x2|的最小值为π求出函数的周期,然后求出ω即可.
解答:
解:函数y=sin(ωx+θ)(ω>0,0<θ<π)为偶函数,所以θ=
,
因为函数图象与直线y=1的交点的横坐标为x1,x2,
若|x1-x2|=kπ,k∈N*,
则|x1-x2|的最小值为π,
所以函数的周期为:π,
所以
=π,所以ω=2,
∴ω×θ=2×
=π.
故答案为:π.
| π |
| 2 |
因为函数图象与直线y=1的交点的横坐标为x1,x2,
若|x1-x2|=kπ,k∈N*,
则|x1-x2|的最小值为π,
所以函数的周期为:π,
所以
| 2π |
| ω |
∴ω×θ=2×
| π |
| 2 |
故答案为:π.
点评:本题是基础题,考查三角函数的解析式的求法,注意三角函数的图象与性质的应用是解题的关键,考查计算能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
设函数f(x)=2cos2x+
sin2x,x∈R,则下列结论正确的是( )
| 3 |
A、f(x)的图象关于直线x=
| ||
| B、f(x)的最大值是2 | ||
C、f(x)在[0,
| ||
D、f(x)的图象关于点(
|
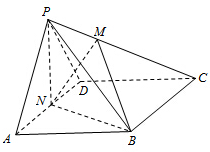 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD