题目内容
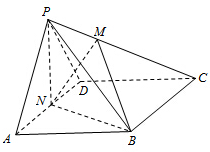如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，PA=PD=AD=2，点M在线段PC上，且
| PM |
| MC |
（1）求证：BC⊥平面PNB
（2）若平面PAD⊥平面ABCD，且二面角M-BN-D为60°，求λ的值．
考点：用空间向量求平面间的夹角,二面角的平面角及求法
专题：空间位置关系与距离,空间角
分析：（1）由已知得PN⊥AD，△ABD为等边三角形，BN⊥AD，从而AD⊥平面PNB，由AD∥BC，能证明BC⊥平面PNB．
（2）分别以NA，NB，NP为x，y，z轴，建立空间直角坐标系，求出平面BMN的一个法向量和平面BCD的一个法向量，由此结合已知条件利用向量法能求出λ的值．
（2）分别以NA，NB，NP为x，y，z轴，建立空间直角坐标系，求出平面BMN的一个法向量和平面BCD的一个法向量，由此结合已知条件利用向量法能求出λ的值．
解答：
解：（1）证明：∵PA=AD，N为AD的中点，
∴PN⊥AD，
又底面ABCD为菱形，∠BAD=60°，
∴△ABD为等边三角形，
又∴N为AD的中点，
∴BN⊥AD，又PN∩BN=N，
∴AD⊥平面PNB，
∵AD∥BC，∴BC⊥平面PNB．
（2）解：∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PN⊥AD，
如图，分别以NA，NB，NP为x，y，z轴，建立空间直角坐标系，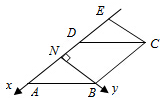
则A（1，0，0），B（0，
，0），
C（-2，
，0），D（-1，0，0），P（0，0，
），
设M（x，y，z），则
=（x，y，z-
），
=（-2-x，
-y，-z），
∴λ
=（-2λ，
λ-λy，-λz），
由
=λ
（0≤λ≤1），得
，
解得x=
，y=
，z=
，
∴M（
，
，
），
∴
=（
，-
，
），
=（0，
，0），
设
=（x，y，z）是平面BMN的一个法向量，
则
，
取z=
，得
=（
，0，
），
又平面BCD的一个法向量为
=（0，0，
），
∵二面角M-BN-D为60°，
∴cos＜
，
＞=
=
=cos60°，
解得λ=
．
∴PN⊥AD，
又底面ABCD为菱形，∠BAD=60°，
∴△ABD为等边三角形，
又∴N为AD的中点，
∴BN⊥AD，又PN∩BN=N，
∴AD⊥平面PNB，
∵AD∥BC，∴BC⊥平面PNB．
（2）解：∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PN⊥AD，
如图，分别以NA，NB，NP为x，y，z轴，建立空间直角坐标系，
则A（1，0，0），B（0，
| 3 |
C（-2，
| 3 |
| 3 |
设M（x，y，z），则
| PM |
| 3 |
| MC |
| 3 |
∴λ
| MC |
| 3 |
由
| PM |
| MC |
|
解得x=
| -2λ |
| λ+1 |
| ||
| λ+1 |
| ||
| λ+1 |
∴M（
| -2λ |
| λ+1 |
| ||
| λ+1 |
| ||
| λ+1 |
∴
| BM |
| -2λ |
| λ+1 |
| ||
| λ+1 |
| ||
| λ+1 |
| NB |
| 3 |
设
| n |
则
|
取z=
| 3 |
| n |
| 3 |
| 2λ |
| 3 |
又平面BCD的一个法向量为
| m |
| 3 |
∵二面角M-BN-D为60°，
∴cos＜
| n |
| m |
| ||||
|
|
| 3 | ||||||
|
解得λ=
| 1 |
| 2 |
点评：本题考查直线与平面垂直的证明，考查满足条件的实数值的求法，解题时要认真审题，注意空间中线线、线面、面面间的位置关系和性质的合理运用，是中档题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
一个多面体的三视图和直观图如图所示，其中M，N分别是AB，SA的中点．