题目内容
6.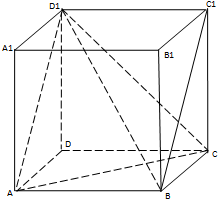 如图在正方体中
如图在正方体中(1)求异面直线BC1与CD1所成的角;
(2)求直线D1B与底面ABCD所成角的正弦值;
(3)求二面角D1-AC-D大小的正切值.
分析 (1)由BC1∥AD1,知∠AD1C即为BC1与CD1所成角,由此能求出BC1与CD1所成角.
(2)利用DD1⊥平面ABCD,可得∠D1DB为直线D1B与平面ABCD所成的角,利用正弦函数可得结论;
(3)连接BD交AC于O,则DO⊥AC,根据正方体的性质,D1D⊥AC,得出AC⊥D1O,∠D1OD为二面角D1-AC-D的平面角,在直角三角形D1OD中求解即可.
解答  解:(1)连接AC,AD1,如图所示:
解:(1)连接AC,AD1,如图所示:
∵BC1∥AD1,
∴∠AD1C即为BC1与CD1所成角,
∵△AD1C为等边三角形,
∴∠AD1C=60°,
故异面直线BC1与CD1所成的角为60°;
(2)∵DD1⊥平面ABCD,
∴∠D1DB为直线D1B与平面ABCD所成的角,
在Rt△D1DB中,sin∠D1DB=$\frac{{D}_{1}D}{{D}_{1}B}$=$\frac{\sqrt{3}}{3}$
∴直线D1B与平面ABCD所成角的正弦值为$\frac{\sqrt{3}}{3}$;
(3)连接BD交AC于O,则DO⊥AC, 根据正方体的性质,D1D⊥面AC,
根据正方体的性质,D1D⊥面AC,
∴D1D⊥AC,D1D∩DO=D,
∴AC⊥面D1OD,∴AC⊥D1O,
∴∠D1OD为二面角D1-AC-D的平面角.
设正方体棱长为1,
在直角三角形D1OD中,DO=$\frac{\sqrt{2}}{2}$,DD1=1,
∴tan∠D1OD=$\sqrt{2}$.
点评 本题考查的知识点是异面直线的夹角,直线与平面的夹角,二面角,难度中档.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.已知正方形ABCD的边长为1,若在正方形内(包括边界)任取一点M,则△ABM的面积不小于$\frac{1}{8}$的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
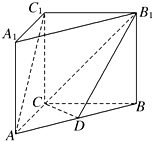 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.