题目内容
18.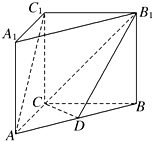 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.(1)求证:AC1∥平面B1CD;
(2)求二面角B-B1C-D的正弦值.
分析 (1)连接BC1交B1C于点E,E为BC1的中点,由为AB的中点,则AC1∥DE,又AC1?平面B1CD,DE?平面B1CD,AC1∥平面B1CD;
(2)AC=BC,D为AB的中点,CD⊥AB,平面ABC⊥平面ABB1A1,可知平面B1CD⊥平面B1BD,过点B作BH⊥B1D,垂足为H,则BH⊥平面B1CD,B1C⊥BE,B1C⊥EH,
∠BEH为二面角B-B1C-D的平面角,Rt△BHE中,BE=$\sqrt{2}$,BH=$\frac{B{B}_{1}•BD}{{B}_{1}D}$=$\frac{2}{\sqrt{3}}$,则sin∠BEH=$\frac{BH}{BE}$=$\frac{\sqrt{6}}{3}$.
解答 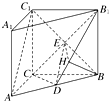 解:(1)证明:如图,连接BC1交B1C于点E,
解:(1)证明:如图,连接BC1交B1C于点E,
则E为BC1的中点.
∵D为AB的中点,∴在△ABC1中,AC1∥DE,
又AC1?平面B1CD,DE?平面B1CD,
∴AC1∥平面B1CD
(2)∵AC=BC,D为AB的中点,
∴CD⊥AB,
又平面ABC⊥平面ABB1A1,
∴CD⊥平面ABB1A1.
∴平面B1CD⊥平面B1BD,
过点B作BH⊥B1D,垂足为H,则BH⊥平面B1CD,
连接EH,
∵B1C⊥BE,B1C⊥EH,
∴∠BEH为二面角B-B1C-D的平面角.
在Rt△BHE中,BE=$\sqrt{2}$,BH=$\frac{B{B}_{1}•BD}{{B}_{1}D}$=$\frac{2}{\sqrt{3}}$,
则sin∠BEH=$\frac{BH}{BE}$=$\frac{\sqrt{6}}{3}$.
即二面角B-B1C-D的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查用空间向量求直线与平面的夹角,直线与平面平行的判定,用空间向量求平面间的夹角,考查空间想象能力,逻辑思维能力,属于中档题.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| Z | 1 | 2 | 3 |
| P | 0.5 | x | y |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
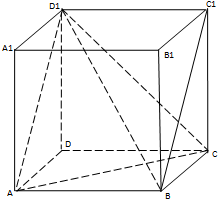 如图在正方体中
如图在正方体中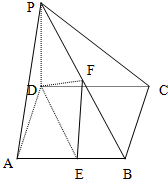 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点