题目内容
已知函数f(x)=x+
(x>0).
(1)若a<0,试用定义证明:f(x)在(0,+∞)上单调递增;
(2)若a>0,当x∈[1,3]时不等式f(x)≥2恒成立,求a的取值范围.
| a |
| x |
(1)若a<0,试用定义证明:f(x)在(0,+∞)上单调递增;
(2)若a>0,当x∈[1,3]时不等式f(x)≥2恒成立,求a的取值范围.
考点:函数恒成立问题,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用函数单调性的定义证明函数为增函数;
(2)若a>0,则f(x)在(0,
)上单调递减,在(
,+∞)上单调递增.分①若0<a≤1,②若1<a<9,③若a≥9,三种情况讨论函数在[1,3]上的单调性,求得函数的最小值,列出不等式,即可得出结论.
(2)若a>0,则f(x)在(0,
| a |
| a |
解答:
解:(1)若a<0,设0<x1<x2<+∞,则
f(x1)-f(x2)=(x1-x2)(1-
).┅(2分)
因为x1-x2<0,1-
>0,所以f(x1)-f(x2)<0,即f(x1)<f(x2),
故,f(x)在(0,+∞)上单调递增.┅(6分)
(2)若a>0,则f(x)在(0,
)上单调递减,在(
,+∞)上单调递增.
①若0<a≤1,则f(x)在[1,3]上单调递增,f(x)min=f(1)=1+a.
所以,1+a≥2,即a≥1,所以a=1.┅(8分)
②若1<a<9,则f(x)在[1,
]上单调递减,在[
,3]上单调递增,
f(x)min=f(
)=2
.所以,2
≥2,a≥1即,所以1<a<9.┅(10分)
③若a≥9,则f(x)在[1,3]上单调递减,f(x)min=f(3)=3+
.
所以,≥2,即a≥-3,所以a≥9.┅(12分)
综合①②③,a≥1.┅(14分)
f(x1)-f(x2)=(x1-x2)(1-
| a |
| x1x2 |
因为x1-x2<0,1-
| a |
| x1x2 |
故,f(x)在(0,+∞)上单调递增.┅(6分)
(2)若a>0,则f(x)在(0,
| a |
| a |
①若0<a≤1,则f(x)在[1,3]上单调递增,f(x)min=f(1)=1+a.
所以,1+a≥2,即a≥1,所以a=1.┅(8分)
②若1<a<9,则f(x)在[1,
| a |
| a |
f(x)min=f(
| a |
| a |
| a |
③若a≥9,则f(x)在[1,3]上单调递减,f(x)min=f(3)=3+
| a |
| 3 |
所以,≥2,即a≥-3,所以a≥9.┅(12分)
综合①②③,a≥1.┅(14分)
点评:本题主要考查函数单调性的证明及应用函数的单调性求函数的最值知识,解题时注意对a的分类讨论思想的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
等比数列{an}中,已知a3=2,a4-a2=
,则前5项和S5=( )
| 2 |
A、7±3
| ||
B、3
| ||
C、7+3
| ||
D、3
|
(2014•温州市高三调研)设函数f(x)=
,那么f(2014)=( )
|
| A、64 | B、16 | C、4 | D、1 |
设集合A={x|x2+2x-3>0},R为实数,Z为整数集,则(CRA)∩Z=( )
| A、{x|-3<x<1} |
| B、{x|-3≤x≤1} |
| C、{-2,-1,0} |
| D、{-3,-2,-1,0,1} |
已知x1,x2是函数f(x)=e-x-|lnx|的两个零点,则( )
A、
| ||
| B、1<x1x2<e | ||
| C、e<x1x2<2e | ||
| D、2e<x1x2<10 |

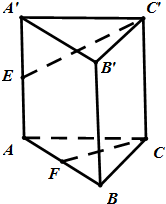 已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.
已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.