题目内容
已知x1,x2是函数f(x)=e-x-|lnx|的两个零点,则( )
A、
| ||
| B、1<x1x2<e | ||
| C、e<x1x2<2e | ||
| D、2e<x1x2<10 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:在同一直角坐标系中作出y=e-x与y=|lnx|的图象,设两函数图象的交点A(x1,-lnx1),B(x2,lnx2),依题意可得-1<lnx1<0,0<lnx2<1,利用对数的运算性质结合图象即可得答案.
解答:
解:f(x)=e-x-|lnx|=0⇒e-x=|lnx|,在同一直角坐标系中作出y=e-x与y=|lnx|的图象,
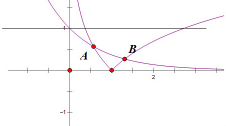
设两函数图象的交点A(x1,-lnx1),B(x2,lnx2),
则0<-lnx1<1,即-1<lnx1<0,
又0<lnx2<1,
所以,-1<lnx1+lnx2<1,即-1<lnx1x2<1,
所以
<x1x2<e①;
又-lnx1>lnx2,故lnx1x2<0,即x1x2<1,②
由①②得:
<x1x2<1,
故选:A.

设两函数图象的交点A(x1,-lnx1),B(x2,lnx2),
则0<-lnx1<1,即-1<lnx1<0,
又0<lnx2<1,
所以,-1<lnx1+lnx2<1,即-1<lnx1x2<1,
所以
| 1 |
| e |
又-lnx1>lnx2,故lnx1x2<0,即x1x2<1,②
由①②得:
| 1 |
| e |
故选:A.
点评:本题考查根的存在性及根的个数判断,依题意可得-1<lnx1<0,0<lnx2<1是关键,考查作图能力与运算求解能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|y=
},B={x|
≤0},则A∩B=( )
| x2-2x-3 |
| x+2 |
| x-2 |
| A、[-1,1] |
| B、[-1,2) |
| C、[1,2) |
| D、[-2,-1] |
不透明的盒子里面装有五个分别标有数字1、2、3、4、5的乒乓球,这些球除数字外,其他完全相同,一位学生随机摸出两个球,两个球的数字之和是偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x2-2|x|-m的零点有两个,求实数m的取值范围( )
| A、-1<m<0 |
| B、m>0或m=-1 |
| C、m>0 或-1≤m<0 |
| D、0<m<1 |