题目内容
已知数列{an}的前n项和为Sn,a1=3,数列{an+Sn}是公差为2的等差数列.
(1)证明数列{an-2}为等比数列;
(2)证明Sn<2(n+1).
(1)证明数列{an-2}为等比数列;
(2)证明Sn<2(n+1).
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由已知条件得an+Sn=3+3+2(n-1)=2n+4,由此推导出2(an-2)=an-1-2,从而能够证明{an-2}是首项为a1-2=1,公比为
的等比数列.
(2)由(1)知an-2=
,所以an=
+2,由此能够证明Sn<2(n+1).
| 1 |
| 2 |
(2)由(1)知an-2=
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
解答:
证明:(1)∵数列{an}的前n项和为Sn,a1=3,
数列{an+Sn}是公差为2的等差数列,
∴an+Sn=3+3+2(n-1)=2n+4,
当n≥2时,由an+Sn=2n+4,得
an-1+Sn-1=2n+2,
两式相减得an-an-1+an=2
∴2(an-2)=an-1-2
∴{an-2}是首项为a1-2=1,公比为
的等比数列.
(2)由(1)知an-2=
,∴an=
+2,
∴Sn=
+2n=2-
+2n
=2(n+1)-
,
∴Sn<2(n+1).
数列{an+Sn}是公差为2的等差数列,
∴an+Sn=3+3+2(n-1)=2n+4,
当n≥2时,由an+Sn=2n+4,得
an-1+Sn-1=2n+2,
两式相减得an-an-1+an=2
∴2(an-2)=an-1-2
∴{an-2}是首项为a1-2=1,公比为
| 1 |
| 2 |
(2)由(1)知an-2=
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
∴Sn=
1-
| ||
1-
|
| 2 |
| 2n |
=2(n+1)-
| 2 |
| 2n |
∴Sn<2(n+1).
点评:本题考查等比数列的证明,考查不等式的证明,解题时要认真审题,注意等比数列性质的合理运用.

练习册系列答案
相关题目
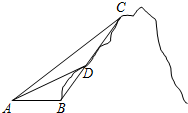 某旅游景点有一座风景秀丽的山峰,游客可以乘长为3km的索道AC上山,也可以沿山路BC上山,山路BC中间有一个距离山脚B为1km的休息点D.已知∠ABC=120°,∠ADC=150°.假设小王和小李徒步攀登的速度为每小时1.2km,请问:两位登山爱好者能否在2个小时内徒步登上山峰(即从B点出发到达C点)
某旅游景点有一座风景秀丽的山峰,游客可以乘长为3km的索道AC上山,也可以沿山路BC上山,山路BC中间有一个距离山脚B为1km的休息点D.已知∠ABC=120°,∠ADC=150°.假设小王和小李徒步攀登的速度为每小时1.2km,请问:两位登山爱好者能否在2个小时内徒步登上山峰(即从B点出发到达C点)