题目内容
过点P（2，3）且与直线2x+y-1=0垂直的直线方程是 ．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：根据已知，与直线2x+y-1=0垂直的直线的斜率为
，从而可求出直线方程为x-2y+4=0．
| 1 |
| 2 |
解答：
解：设所求直线斜率为k，
∵直线2x+y-1=0的斜率为-2，且所求直线与直线2x+y-1=0垂直
∴k=
．
又∵直线过点P（2，3），
∴所求直线方程为
y-3=
（x-2），
即x-2y+4=0．
故答案为：x-2y+4=0．
∵直线2x+y-1=0的斜率为-2，且所求直线与直线2x+y-1=0垂直
∴k=
| 1 |
| 2 |
又∵直线过点P（2，3），
∴所求直线方程为
y-3=
| 1 |
| 2 |
即x-2y+4=0．
故答案为：x-2y+4=0．
点评：本题考查直线的点斜式方程以及两直线相互垂直的性质等知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若如图所示的程序框图输出的S是31，则在判断框中M表示的“条件”应该是（ ）| A、n≥3 | B、n≥4 |
| C、n≥5 | D、n≥6 |
同时投掷两个骰子，则向上的点数之差的绝对值为4的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线f（x）=2x在x=0处的切线方程为（ ）
| A、y=x-1 |
| B、y=x+1 |
| C、y=（x-1）ln2 |
| D、y=xln2+1 |
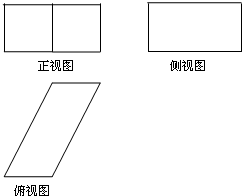一个几何体的三视图如图所示．已知正视图为两个边长为1的正方形拼成的矩形，侧视图是一个长为