题目内容
已知函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,
(1)求a、b的值;
(2)设函数f(x)=
,试判断f(x)在区间[2,3]上的单调性并证明.
(1)求a、b的值;
(2)设函数f(x)=
| g(x) |
| x |
考点:二次函数在闭区间上的最值
专题:综合题,函数的性质及应用
分析:(1)根据函数g(x)=ax2-2ax+1+b(a≠0,b<1),可知函数在区间[2,3]上是单调函数,故可建立方程组,从而可求a、b的值;
(2)利用导数判断并证明f(x)在区间[2,3]上的单调递增.
(2)利用导数判断并证明f(x)在区间[2,3]上的单调递增.
解答:
解:(1)g(x)=ax2-2ax+1+b,函数的对称轴为直线x=1,由题意得:
①
得a=1,b=0;
②
得a=-1,b=3>1(舍去)
∴a=1,b=0;
(2)g(x)=x2-2x+1,f(x)=
=x+
-2,
∴f′(x)=1-
,
∵x∈[2,3],
∴f′(x)>0,
∴f(x)在区间[2,3]上的单调递增.
①
|
②
|
∴a=1,b=0;
(2)g(x)=x2-2x+1,f(x)=
| g(x) |
| x |
| 1 |
| x |
∴f′(x)=1-
| 1 |
| x2 |
∵x∈[2,3],
∴f′(x)>0,
∴f(x)在区间[2,3]上的单调递增.
点评:本题考查函数的单调性,考查函数的最值,考查函数与方程思想,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
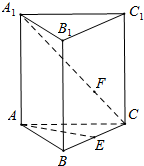 如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合.
如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合. 如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC