题目内容
11.已知双曲线Γ:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一条渐近线为l,圆C:(x-a)2+y2=8与l交于A,B两点,若△ABC是等腰直角三角形,且$\overrightarrow{OB}=5\overrightarrow{OA}$(其中O为坐标原点),则双曲线Γ的离心率为( )| A. | $\frac{{\sqrt{13}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{3}$ | C. | $\frac{{\sqrt{13}}}{5}$ | D. | $\frac{{2\sqrt{13}}}{5}$ |
分析 求出双曲线的渐近线方程,圆的圆心与半径,利用距离推出ab关系式,然后求解离心率即可.
解答 解:如图.依题意,在△RtACB中,BC=AC=2$\sqrt{2}$,
∴AB=4,又$\overrightarrow{OB}=5\overrightarrow{OA}$(其中O为坐标原点),∴OB=5
在△OCB中,由余弦定理得a=OC=$\sqrt{B{C}^{2}+O{B}^{2}-2BC•OBcos4{5}^{0}}=\sqrt{13}$.
因为点C(a,0)到渐进线y=$\frac{b}{a}x$的距离为2,即$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}=2$.
解得b=$\frac{2\sqrt{13}}{3}$,即得e2=1+$\frac{{b}^{2}}{{a}^{2}}$=$\frac{13}{9}$,∴双曲线Γ的离心率为$\frac{\sqrt{13}}{3}$.
故选:A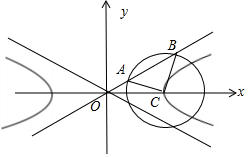
点评 本题考查双曲线的简单性质的应用,直线与圆的位置关系的应用,考查计算能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
1.已知Sn是等差数列{an}的前n项和,则2(a1+a3+a5)+3(a8+a10)=36,则S11=( )
| A. | 66 | B. | 55 | C. | 44 | D. | 33 |
2.在区间[0,1]上随机取两个数,则这两个数之和小于$\frac{3}{2}$的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
16.若f(x)+${∫}_{0}^{1}$f(x)dx=x,则${∫}_{0}^{1}$f(x)dx=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
1.对于椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$,下面说法正确的是( )
| A. | 长轴长为2 | B. | 短轴长为3 | C. | 离心率为$\frac{1}{2}$ | D. | 焦距为1 |
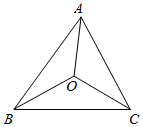 如图,已知O为△ABC的外心,角A、B、C的对边分别为a、b、c.
如图,已知O为△ABC的外心,角A、B、C的对边分别为a、b、c.