题目内容
7.已知数列{an}的前n项和为Sn,若函数f(x)=sinx+$\sqrt{3}$cosx(x∈R)的最大值为a1,且满足an-anSn+1=$\frac{{a}_{1}}{2}$-anSn,则数列{an}的前2017项之积A2017=2.分析 函数f(x)=sinx+$\sqrt{3}$cosx=2$sin(x+\frac{π}{3})$≤2,可得a1=2.由an-anSn+1=$\frac{{a}_{1}}{2}$-anSn,可得an=1+anan+1,n≥2时,an-1anan+1=an-1an-an-1=-1.即可得出数列{an}的前2017项之积A2017=A672×3+1.
解答 解:函数f(x)=sinx+$\sqrt{3}$cosx=2$sin(x+\frac{π}{3})$≤2,∴a1=2.
∵an-anSn+1=$\frac{{a}_{1}}{2}$-anSn,∴an=1+an(Sn+1-Sn),∴an=1+anan+1,
∴anan+1=an-1,
∴n≥2时,an-1anan+1=an-1an-an-1=-1.
∴数列{an}的前2017项之积A2017=A672×3+1=a1×(-1)672=2.
故答案为:2.
点评 本题考查了数列递推关系、三角函数求值、法则求积,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
18.为了了解甲、乙两所学校全体高三年级学生在该地区八校联考中的数学成绩情况,从两校各随机抽取60名学生,将所得样本作出频数分布统计表如下:
甲校:
乙校:
以抽样所得样本数据估计总体
(1)比较甲、乙两校学生的数学平均成绩的高低;
(2)若规定数学成绩不低于120分为优秀,从甲、乙两校全体高三学生中各随机抽取2人,其中数学成绩为优秀的共X人,求X的分布列及数学期望.
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 5 | 9 | 10 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 14 | 10 | 6 | 4 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 4 | 8 | 16 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | 6 | 6 | 3 |
(1)比较甲、乙两校学生的数学平均成绩的高低;
(2)若规定数学成绩不低于120分为优秀,从甲、乙两校全体高三学生中各随机抽取2人,其中数学成绩为优秀的共X人,求X的分布列及数学期望.
2.在区间[0,1]上随机取两个数,则这两个数之和小于$\frac{3}{2}$的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
12.“x≥2”是“log2x2≥2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条条 |
16.若f(x)+${∫}_{0}^{1}$f(x)dx=x,则${∫}_{0}^{1}$f(x)dx=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
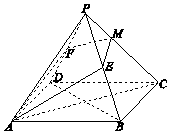 如图,在正四棱锥P-ABCD中,PA=AB,E,F分别为PB,PD的中点.
如图,在正四棱锥P-ABCD中,PA=AB,E,F分别为PB,PD的中点.