题目内容
观察下列等式：
=1，
=
，
=
，
=
，…，则第n个等式为 ．
| 12 |
| 1 |
| 12+22 |
| 1+2 |
| 5 |
| 3 |
| 12+22+32 |
| 1+2+3 |
| 7 |
| 3 |
| 12+22+32+42 |
| 1+2+3+4 |
| 9 |
| 3 |
考点：归纳推理
专题：推理和证明
分析：根据题意观察可知．
解答：
解：∵
=1，
=
，
=
，
=
，…，
可以推测，左边的分数的分子是数字的从1开始连续数的平方和，分母是从1开始连续数的和，右边分子式奇数，分母是所在等式的个数，
故第n个等式为式为：
=
．
故答案为：
=
．
| 12 |
| 1 |
| 12+22 |
| 1+2 |
| 5 |
| 3 |
| 12+22+32 |
| 1+2+3 |
| 7 |
| 3 |
| 12+22+32+42 |
| 1+2+3+4 |
| 9 |
| 3 |
可以推测，左边的分数的分子是数字的从1开始连续数的平方和，分母是从1开始连续数的和，右边分子式奇数，分母是所在等式的个数，
故第n个等式为式为：
| 12+22+32+42+…+n2 |
| 1+2+3+4+…+n |
| 2n+1 |
| 3 |
故答案为：
| 12+22+32+42+…+n2 |
| 1+2+3+4+…+n |
| 2n+1 |
| 3 |
点评：本题主要考查了归纳推理的问题，关键是找到相对应的数字的规律，属于基础题．
练习册系列答案
相关题目
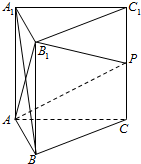如图，已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点．
将全体正整数按如图规律排成一个三角形数阵，若数2014在图中第m行从左往右数的第n位．则（m，n）为