题目内容
已知函数f(x)=
sin2x+sinxcosx.
(1)求函数f(x)在区间[
,π]上的零点;
(2)设g(x)=f(x)-
sin2x,求函数g(x)的图象的对称轴方程.
| 3 |
(1)求函数f(x)在区间[
| π |
| 2 |
(2)设g(x)=f(x)-
| 3 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)令f(x)=0,根据函数解析式求得sinx=0或tanx=-
,分别求得x的值综合可得答案.
(2)先求得g(x)的解析式,进而根据正弦函数的图象和性质求得其对称轴方程.
| ||
| 3 |
(2)先求得g(x)的解析式,进而根据正弦函数的图象和性质求得其对称轴方程.
解答:
解:(1)令f(x)=0,得sinx(
sinx+cosx)=0,
所以sinx=0,tanx=-
.
由sinx=0,x∈[
,π],得x=π,
由tanx=-
,x∈[
,π],
得x=
,
综上,f(x)的零点为x=π或x=
.
(2)g(x)=sinxcosx=
sin2x,
由2x=kx+
(k∈Z)得x=
+
(k∈Z),
即函数g(x)的图象的对称轴方程为:x=
+
(k∈Z).
| 3 |
所以sinx=0,tanx=-
| ||
| 3 |
由sinx=0,x∈[
| π |
| 2 |
由tanx=-
| ||
| 3 |
| π |
| 2 |
得x=
| 5π |
| 6 |
综上,f(x)的零点为x=π或x=
| 5π |
| 6 |
(2)g(x)=sinxcosx=
| 1 |
| 2 |
由2x=kx+
| π |
| 2 |
| kπ |
| 2 |
| π |
| 4 |
即函数g(x)的图象的对称轴方程为:x=
| kπ |
| 2 |
| π |
| 4 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.利用数形结合的思想,与三角函数图象相联系解决问题较直观.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.下列各对事件中,为对立事件的是( )
| A、恰有一名男生和恰有2名男生 |
| B、至少一名男生和至少一名女生 |
| C、至少有一名男生和与全是女生 |
| D、至少有一名男生和全是男生 |
已知平面向量
=(λ,-2),
=(4,1),若
∥
,则实数λ等于( )
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
| C、-8 | ||
| D、8 |
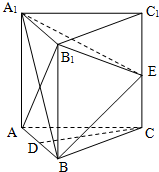 如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.