题目内容
15.已知奇函数f(x)的定义域为(-∞,0)∪(0,+∞),当x>0时,f(x)=ln(|x-1|+1),则函数f(x)的图象大致为( )| A. | 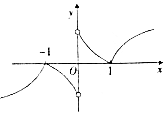 | B. | 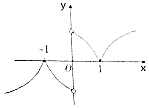 | ||
| C. | 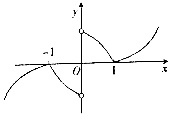 | D. | 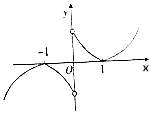 |
分析 当0<x<1时,f(x)=ln(2-x),函数f(x)在(0,1)上单调递减,当x≥1时,f(x)=lnx,函数f(x)在[1,+∞)单调递增,再根据图象的变化趋势即可判断.
解答 解:当x>0时,f(x)=ln(|x-1|+1),
∴当0<x<1时,f(x)=ln(1-x+1)=ln(2-x),函数f(x)在(0,1)上单调递减,
∴当x≥1时,f(x)=ln(x-1+1)=lnx,函数f(x)在[1,+∞)单调递增,且当x→+∞时,函数值的变化越来越平缓,故排除C,D,
∵函数f(x)=ln(2-x)在(0,1)的图象与f(x)=ln(x)在(1,2)上图象关于x=1对称,故排除A,
故选:B
点评 本题考查了函数的图象的识别和函数的奇偶性的性质,以及函数的单调性,属于中档题.

练习册系列答案
相关题目
5.已知集合A={x|log2x<4},集合B={x||x|≤2},则A∩B=( )
| A. | (0,2] | B. | [0,2] | C. | [-2,2] | D. | (-2,2) |
3.△ABC中,a、b、c分别是三内角A、B、C的对边,且a=4,b+c=5,tanA+tanB+$\sqrt{3}$=$\sqrt{3}$tanA•tanB,则△ABC的面积为( )
| A. | $\frac{3}{2}$ | B. | $3\sqrt{3}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\frac{5}{2}$ |
10.集合{x∈N*|x-3<2}用列举法可表示为( )
| A. | {x<5} | B. | {1,2,3,4} | C. | {0,1,2,3,4,5} | D. | {1,2,3,4,5} |
4.下列函数在[0,$\frac{π}{2}$]上是增函数的是( )
| A. | y=sin2x-cos2x | B. | y=sin2x+cos2x | C. | y=sin2x-2cosx | D. | y=sin2x+2cosx |