题目内容
已知f（x）=x2-1，g（x）=
，求f[g（x）]的表达式．
|
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：根据复合函数之间的关系直接代入即可得到函数的表达式．
解答：
解：当x≥0时，g（x）=x-1，
∴此时f[g（x）]=f（x-1）=（x-1）2-1=x2-2x，
x＜0时，g（x）=2-x，
∴此时f[g（x）]=f（2-x）=（2-x）2-1=x2-4x+3，
∴f[g（x）]=
．
∴此时f[g（x）]=f（x-1）=（x-1）2-1=x2-2x，
x＜0时，g（x）=2-x，
∴此时f[g（x）]=f（2-x）=（2-x）2-1=x2-4x+3，
∴f[g（x）]=
|
点评：本题主要考查函数表达式的求法，利用直接代入法是解决复合函数解析式的常用方法．
练习册系列答案
相关题目
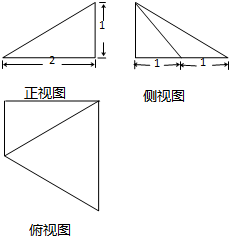某几何体的三视图如图所示，其中正（主）视图与侧（左）视图的边界均为直角三角形，俯视图的边界为直角梯形，则该几何体的体积是（ ）