在等比数列{an}中.a1=1.a3=2a2.数列{an}前n项和Sn为( )A．Sn=2n-1B．Sn=2n-1C．Sn=n2D．Sn=2n-1 题目和参考答案——青夏教育精英家教网—

题目内容

1．在等比数列{a_n}中，a₁=1，a₃=2a₂，数列{a_n}前n项和S_n为（　　）

A．

S_n=2^n-1

B．

S_n=2n-1

C．

S_n=n²

D．

S_n=2ⁿ-1

分析利用等比数列通项公式求出公比q=2，由此能求出数列{a_n}前n项和S_n．

解答解：∵在等比数列{a_n}中，a₁=1，a₃=2a₂，
∴1×q²=2×1×q．
解得q=2，
∴数列{a_n}前n项和S_n=$\frac{1×（1-{2}^{n}）}{1-2}$=2ⁿ-1．
故选：D．

点评本题考查等比数列的通项公式、前n项和公式等基础知识，考查考查推理论证能力、运算求解能力、抽象概括能力，考查转化化归思想、分类讨论思想、函数与方程思想，考查创新意识、应用意识，是基础题．

练习册系列答案

相关题目

11．

如图，在一段直行的公路上方D处有一测速球机，在球机下方路面有A，B，C三个测速点，测得球机距点A为14米，AB=10米，球机探测点B和C的俯角分别为60°和45°，现有一小汽车从A地到C地用时1秒，则小汽车经过AC这段路程的平均速度约为18.1米/秒．（结果精确到0.1，参考数据$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）

12．朱世杰是历史上最伟大的数学家之一，他所著的《四元玉鉴》卷中“如像招数”五问有如下问题：“今有官司差夫一千八百六十四人筑堤．只云初日差六十四人，次日转多七人，每人日支米三升，共支米四百三石九斗二升，问筑堤几日”．其大意为：“官府陆续派遣1864人前往修筑堤坝，第一天派出64人，从第二天开始，每天派出的人数比前一天多7人，修筑堤坝的每人每天分发大米3升，共发出大米40392升，问修筑堤坝多少天”．这个问题中，前5天应发大米（　　）

9．设sin（π-θ）=$\frac{1}{3}$，则cos2θ=（　　）

A．

$\frac{7}{9}$

B．

$-\frac{4\sqrt{2}}{9}$

C．

$-\frac{7}{9}$

D．

$±\frac{4\sqrt{2}}{9}$

16．已知抛物线C：y²=8x的焦点为F，准线l与x轴的交点为M，过点M的直线l′与抛物线C的交点为P，Q，延长PF交抛物线C于点A，延长QF交抛物线C于点B，若$\frac{|PF|}{|AF|}$+$\frac{|QF|}{|BF|}$=22，则直线l′的方程为y=±$\frac{\sqrt{6}}{6}$（x+2）．

6．

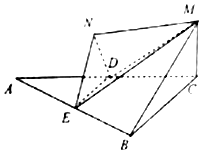已知如图，△ABC是边长为4的等边三角形，MC⊥平面ABC，D、E分别是线段AC、AB的中点，将△ADE沿DE翻折至△NDE，平面NDE⊥平面ABC．
（Ⅰ）求证：平面BCM∥平面EDN；
（Ⅱ）求三棱锥M-EDN的体积V．

3．设集合A={x|f（x）=x}，B={x|f[f（x）]=x}，设f（x）=x²-（2a-1）x+a²（常数a∈R），求证：A=B．

20．设函数f（x）=$\frac{{x}^{3}}{3}$-$\frac{3a+2}{2}$x²+6ax+b，其中a，b∈R．
（1）若函数f（x）在x=1处取得极值-$\frac{1}{6}$，求a，b的值；
（2）求函数f（x）的单调递增区间．

1．若函数$f（x）=3+\frac{{{2^x}-1}}{{{2^x}+1}}+sin2x$在区间[-k，k]（k＞0）上的值域为[m，n]，则m+n等于（　　）

试题分类