题目内容
 如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影恰好是AB的中点O,底面ABC是正三角形,其重心为G点,D是BC中点,B1D交BC1于E.
如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影恰好是AB的中点O,底面ABC是正三角形,其重心为G点,D是BC中点,B1D交BC1于E.(1)求证:GE∥侧面AA1B1B;
(2)若二面角B1-AD-B的正切值为
2
| ||
| 3 |
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结AB1,则
=
=
,由此能证明GE∥侧面AA1B1B.
(2)过B1作B1F⊥AB,交AB延长线于F,过F作AD的垂线,交AD延长线于E,连B1E,则∠B1EF为二面角B1-AD-B的平面角,从而tan∠B1EF=
,设正三角形ABC边长为a,连OD并延长到H,使DH=OD,∠C1BH为直线BC1与底面ABC所成角,由此能求出直线BC1与底面ABC所成角.
| DE |
| EB1 |
| DG |
| GA |
| 1 |
| 2 |
(2)过B1作B1F⊥AB,交AB延长线于F,过F作AD的垂线,交AD延长线于E,连B1E,则∠B1EF为二面角B1-AD-B的平面角,从而tan∠B1EF=
2
| ||
| 3 |
解答:
(1)证明:
=
=
,连结AB1,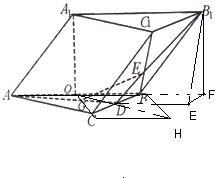
∵
=
=
,GE不包含于AB1,AB1?平面AA1B1B,
∴GE∥侧面AA1B1B.
(2)过B1作B1F⊥AB,交AB延长线于F,
过F作AD的垂线,交AD延长线于E,
连B1E,则∠B1EF为二面角B1-AD-B的平面角,
从而tan∠B1EF=
,
设正三角形ABC边长为a,则
=
=
,
∴EF=
DB=
a,
则B1F =A1O=
a•
=
a,从而AA1=AB,
连OD并延长到H,使DH=OD,
则OH
A1C1,故四边形A1OHC1为平行四边形,
∴C1H⊥平面ABC,∠C1BH为直线BC1与底面ABC所成角,
∵OH与BC互相平分,∴四边形OCHB为平行四边形,
∴BH=OC=
a,
∴△C1HB为等腰直角三角形,
∴直线BC1与底面ABC所成角为
.
| DE |
| EB1 |
| BD |
| B1C1 |
| 1 |
| 2 |

∵
| DE |
| EB1 |
| DG |
| GA |
| 1 |
| 2 |
∴GE∥侧面AA1B1B.
(2)过B1作B1F⊥AB,交AB延长线于F,
过F作AD的垂线,交AD延长线于E,
连B1E,则∠B1EF为二面角B1-AD-B的平面角,
从而tan∠B1EF=
2
| ||
| 3 |
设正三角形ABC边长为a,则
| EF |
| DB |
| AF |
| AB |
| 3 |
| 2 |
∴EF=
| 3 |
| 2 |
| 3 |
| 4 |
则B1F =A1O=
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
连OD并延长到H,使DH=OD,
则OH
| ∥ |
. |
∴C1H⊥平面ABC,∠C1BH为直线BC1与底面ABC所成角,
∵OH与BC互相平分,∴四边形OCHB为平行四边形,
∴BH=OC=
| ||
| 2 |
∴△C1HB为等腰直角三角形,
∴直线BC1与底面ABC所成角为
| π |
| 4 |
点评:本题考查直线与平面垂直的证明,考查直线与底面所成角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
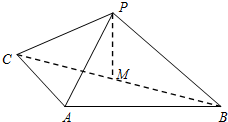 如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.
如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.