题目内容
（文科做）已知函数f（x）=lnx+a，g（x）=ax，a∈R．
（1）若a=1，设函数F(x)=
，求F（x）的极大值；
（2）设函数G（x）=f（x）-g（x），讨论G（x）的单调性．
（1）若a=1，设函数F(x)=
| f(x) |
| g(x) |
（2）设函数G（x）=f（x）-g（x），讨论G（x）的单调性．
考点：利用导数研究函数的极值,利用导数研究函数的单调性
专题：综合题,导数的综合应用
分析：（1）求导数，确定函数的单调性，即可求F（x）的极大值；
（2）求导数，分类讨论，利用导数的正负，即可得出函数的单调性．
（2）求导数，分类讨论，利用导数的正负，即可得出函数的单调性．
解答：
解：（1）当a=1时，F(x)=
，定义域为x∈（0，+∞），
则F′(x)=
．…（2分）
令F'（x）=0得x=1，列表：…（4分）
当x=1时，F（x）取得极大值F（1）=1．…（7分）
（2）G（x）=lnx+a-ax（x＞0），∴G′(x)=
-a=
，x＞0． …（9分）
若a≤0，G'（x）＞0，G（x）在（0，+∞）上递增； …（11分）
若a＞0，当x∈(0，
)时，G'（x）＞0，G（x）单调递增；
当x∈(
，+∞)时，G'（x）＜0，G（x）单调递减． …（14分）
∴当a≤0时，G（x）的增区间为（0，+∞），
当a＞0时，G（x）的增区间为(0，
)，减区间为(
，+∞)． …（16分）
| lnx+1 |
| x |
则F′(x)=
| -lnx |
| x2 |
令F'（x）=0得x=1，列表：…（4分）
| x | （0，1） | 1 | （1，+∞） |
| F'（x） | + | 0 | - |
| F（x） | ↗ | 极大值 | ↘ |
（2）G（x）=lnx+a-ax（x＞0），∴G′(x)=
| 1 |
| x |
| 1-ax |
| x |
若a≤0，G'（x）＞0，G（x）在（0，+∞）上递增； …（11分）
若a＞0，当x∈(0，
| 1 |
| a |
当x∈(
| 1 |
| a |
∴当a≤0时，G（x）的增区间为（0，+∞），
当a＞0时，G（x）的增区间为(0，
| 1 |
| a |
| 1 |
| a |
点评：本题考查利用导数研究函数的极值，考查函数的单调性，正确求导是关键．
练习册系列答案
名师指导一卷通系列答案
相关题目
不等式|x-1|≥2的解集为（ ）
| A、{x|x≤-1或x≥3} |
| B、{x|x≥3} |
| C、{x|-1≤x≤3} |
| D、R |
如图，三棱锥P-ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=4，E为PC的中点，M为AB的中点，点F在PA上，且AF=2FP．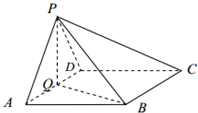
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
已知等腰Rt△ABC，BC⊥AC，将△ABC绕着边AB旋转θ角到△ABC′，连接CC′，D为线段CC′的中点，P是线段AB上任一点．