题目内容
已知函数f(x)=sinx+lnx-kx(k>0).
(Ⅰ)若f(x)在(0,
]上单调递增,求k的取值范围;
(Ⅱ)设g(x)=sinx(x>0),若y=g(x)的图象在y=f(x)的图象上方,求k的取值范围;
(Ⅲ)设n∈N+,证明:
(4-
)<
sin(
)i-1<
+1+
ln2-(
)n+1.
(Ⅰ)若f(x)在(0,
| π |
| 2 |
(Ⅱ)设g(x)=sinx(x>0),若y=g(x)的图象在y=f(x)的图象上方,求k的取值范围;
(Ⅲ)设n∈N+,证明:
| 1 |
| π |
| 1 |
| 2n-1 |
| n+1 |
 |
| i=1 |
| 1 |
| 2 |
(
| ||
| 2 |
| n(n+1) |
| 2 |
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:计算题,证明题,导数的综合应用,不等式
分析:(Ⅰ) 由题意,f′(x)=cosx+
-k≥0,则k≤cosx+
,(cosx+
)min即可;
(Ⅱ) 由题意得x>0时,g(x)>f(x)恒成立,化为lnx-kx<0(x>0)恒成立,h(x)=lnx-kx,利用导数求其最大值即可;
(Ⅲ)显然sinx>
x(0<x<
),则
sin(
)i-1>
[1+(
)+(
)2+…+(
)n];再证明sinx<
+
x-lnx(0<x≤1)成立,从而得证.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
(Ⅱ) 由题意得x>0时,g(x)>f(x)恒成立,化为lnx-kx<0(x>0)恒成立,h(x)=lnx-kx,利用导数求其最大值即可;
(Ⅲ)显然sinx>
| 2 |
| π |
| π |
| 2 |
| n+1 |
 |
| i=1 |
| 1 |
| 2 |
| 2 |
| π |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ) 由题意,f′(x)=cosx+
-k≥0,则k≤cosx+
,
而cosx+
在(0,
]上单调递减,求
则(cosx+
)min=cos
+
=
,则k∈(0,
];
(Ⅱ) 由题意得x>0时,g(x)>f(x)恒成立,
则lnx-kx<0(x>0)恒成立,
令h(x)=lnx-kx,h′(x)=
-k,
x∈(0,
)时,h′(x)>0,
x∈(
,+∞)时,h′(x)<0,
则hmax(x)=h(
)=ln
-1<0,
则k>
.
(Ⅲ)证明:如图,显然sinx>
x(0<x<
),
则
sin(
)i-1>
[1+(
)+(
)2+…+(
)n]
=
(4-
);
由0<(
)i-1≤1,
由(Ⅰ)知,k=
时,f(x)在(0,1]上单调递增.
当0<x≤1时,有sinx+lnx-
x≤sin1-
<
,
则sinx<
+
x-lnx(0<x≤1)成立,
sin(
)i-1<
(n+1)+
[1+(
)+(
)2+…+(
)n]-ln(
)1+2+…+n
=
+1+
ln2-(
)n+1.
即
(4-
)<
sin(
)i-1<
+1+
ln2-(
)n+1.
| 1 |
| x |
| 1 |
| x |
而cosx+
| 1 |
| x |
| π |
| 2 |
则(cosx+
| 1 |
| x |
| π |
| 2 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
(Ⅱ) 由题意得x>0时,g(x)>f(x)恒成立,
则lnx-kx<0(x>0)恒成立,
令h(x)=lnx-kx,h′(x)=
| 1 |
| x |
x∈(0,
| 1 |
| k |
x∈(
| 1 |
| k |
则hmax(x)=h(
| 1 |
| k |
| 1 |
| k |
则k>
| 1 |
| e |
(Ⅲ)证明:如图,显然sinx>
| 2 |
| π |
| π |
| 2 |
则
| n+1 |
 |
| i=1 |
| 1 |
| 2 |
| 2 |
| π |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| π |
| 1 |
| 2n-1 |
由0<(
| 1 |
| 2 |
由(Ⅰ)知,k=
| 1 |
| 2 |
当0<x≤1时,有sinx+lnx-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
则sinx<
| ||
| 2 |
| 1 |
| 2 |
| n+1 |
 |
| i=1 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
(
| ||
| 2 |
| n(n+1) |
| 2 |
| 1 |
| 2 |
即
| 1 |
| π |
| 1 |
| 2n-1 |
| n+1 |
 |
| i=1 |
| 1 |
| 2 |
(
| ||
| 2 |
| n(n+1) |
| 2 |
| 1 |
| 2 |
点评:本题考查了导数的综合应用及恒成立问题化成最值问题的处理方法,同时考查了放缩法证明不等式的变形应用,属于难题.

练习册系列答案
相关题目
函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则实数a的范围是( )
| A、a≤-3 | B、a≤5 |
| C、a≥3 | D、a≥5 |
在下列关于点P,直线l、m与平面α、β的命题中,正确的是( )
| A、若m⊥α,l⊥m,则l∥α |
| B、若α⊥β,α∩β=m,P∈α,P∈l,且l⊥m,则l⊥β |
| C、若l,m是异面直线,m?α,m∥β,l?β,l∥α,则α∥β |
| D、若α⊥β,且l⊥β,m⊥l,则m⊥α |
函数f(x)=2-x的大致图象为( )
A、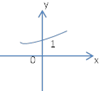 |
B、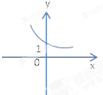 |
C、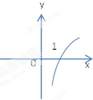 |
D、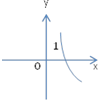 |
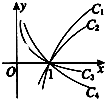 已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为
已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为