题目内容
双曲线
-y2=1的焦距为（ ）
| x2 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
考点：双曲线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：利用双曲线的简单性质求解．
解答：
解：∵双曲线
-y2=1，
∴c=
=2，
∴双曲线
-y2=1的焦距2c=4．
故选：D．
| x2 |
| 3 |
∴c=
| 3+1 |
∴双曲线
| x2 |
| 3 |
故选：D．
点评：本题考查双曲线的焦距的求法，解题时要认真审题，注意双曲线的简单性质的灵活运用．
练习册系列答案
相关题目
反证法证明三角形的内角中至少有一个不小于60°，反设正确的是（ ）
| A、假设三内角都不大于60° |
| B、假设三内角都小于60° |
| C、假设三内角至多有一个大于60° |
| D、假设三内角至多有两个小于60° |
如图，已知⊙O的两条弦AB、CD相交于AB的中点E，且AB=4，DE=CE+3，则CD的长为（ ）| A、4cm | B、2cm |
| C、5cm | D、6cm |
已知数列{an}的通项公式an=logn+1（n+2）（n∈N+），记Jn=a1•a2•a3•…•an为数列{an}的前n项积．定义能使Jn为整数的正整数n为劣数，则在区间（1，2014）内所有的劣数和为（ ）
| A、2026 | B、2046 |
| C、1024 | D、1022 |
从12个产品（其中10个是正品，2个是次品）中任意抽取3个．给出下列四个事件：①3个都是正品；②至少有1个是次品；③3个都是次品；④至少有1个是正品，其中为随机事件的是（ ）
| A、①② | B、①③ | C、②③ | D、②④ |
过椭圆C：
（θ为参数）的右焦点F作直线l交C于M，N两点，|MF|=m，|NF|=n，则
+
的值为（ ）
|
| 1 |
| m |
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
如图，AB是半圆O的直径，弦AD、BC相交于点P，若∠DPB=α，则
=（ ）
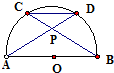
| CD |
| AB |
| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|