题目内容
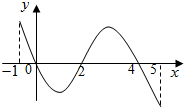 已知函数f(x)的定义域为[-1,5],部分对应值如下表:
已知函数f(x)的定义域为[-1,5],部分对应值如下表:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
①函数f(x)是周期函数;
②函数f(x)在[0,2]上不单调;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a可能有3个零点.
其中判断正确的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:导数的综合应用
分析:根据函数单调性和导数之间的关系,判断函数的单调性和极值情况,即可得到结论.
解答:
解:由导数图象可知,当-1≤x<0和2<x<4,时,f′(x)>0,此时函数单调递增,当0<x<2和4<x≤5,时,f′(x)<0,此时函数单调递减,
即当x=0或x=4时,函数f(x)取得极大值f(0)=f(4)=2,
当x=2时,函数f(x)取得极小值f(2),
则①函数f(x)不是周期函数,故①错误.
②当0<x<2,f′(x)<0,此时函数单调递减,故②错误.
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5,故③错误.
④当1<a<2时,f′(x)<0,此时函数单调递减,则y=f(x)-a最多有一个零点,故④错误,
故正确的为0个,
故选:A.
即当x=0或x=4时,函数f(x)取得极大值f(0)=f(4)=2,
当x=2时,函数f(x)取得极小值f(2),
则①函数f(x)不是周期函数,故①错误.
②当0<x<2,f′(x)<0,此时函数单调递减,故②错误.
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5,故③错误.
④当1<a<2时,f′(x)<0,此时函数单调递减,则y=f(x)-a最多有一个零点,故④错误,
故正确的为0个,
故选:A.
点评:本题主要考查与导数有关的命题的真假判断.利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
从12个产品(其中10个是正品,2个是次品)中任意抽取3个.给出下列四个事件:①3个都是正品;②至少有1个是次品;③3个都是次品;④至少有1个是正品,其中为随机事件的是( )
| A、①② | B、①③ | C、②③ | D、②④ |
过椭圆C:
(θ为参数)的右焦点F作直线l交C于M,N两点,|MF|=m,|NF|=n,则
+
的值为( )
|
| 1 |
| m |
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
掷一枚均匀的硬币3次,出现正面的次数多于反面的次数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知|
|=6,|
|=4,则|
|的取值范围为( )
| AB |
| AC |
| BC |
| A、(2,8) |
| B、[2,8] |
| C、(2,10) |
| D、[2,10] |
在△ABC中,cos2
=
(a,b,c分别是角A,B,C的对边),则△ABC的形状为( )
| A |
| 2 |
| b+c |
| 2c |
| A、等腰直角三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等边三角形 |
如图,AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,则
=( )
| CD |
| AB |

| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
已知命题p:函数y=x3为R上的奇函数;命题q:若b2=ac,则a,b,c一定成等比数列.下列说法正确的是( )
| A、p或q为假 |
| B、p且q为真 |
| C、¬p且q为真 |
| D、¬p或q为假 |