题目内容
17.“a+b<0”是“a与b均为负数的”( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 根据充分必要条件的定义结合不等式的性质判断即可.
解答 解:若a=1,b=-2,满足a+b<0,但不满足a与b均为负数,不是充分条件,
由a与b均为负数,得到a+b<0,是必要条件,
故选:B.
点评 本题考查了充分必要条件,考查不等式的性质,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.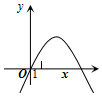 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )| A. | p>q | B. | p=q | ||
| C. | p<q | D. | p,q大小关系不能确定 |
5.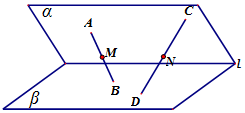 已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )
已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )
 已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )
已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )| A. | 当|CD|=2|AB|时,M,N不可能重合 | |
| B. | M,N可能重合,但此时直线AC与l不可能相交 | |
| C. | 当直线AB,CD相交,且AC∥l时,BD可与l相交 | |
| D. | 当直线AB,CD异面时,MN可能与l平行 |
9.已知cos($\frac{π}{2}$+α)=$\frac{3}{5}$,则α∈($\frac{π}{2}$,$\frac{3π}{2}$),则sin2α=( )
| A. | -$\frac{24}{25}$ | B. | -$\frac{16}{25}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≤3\\ x+3y≥-k\\ y≤1\end{array}\right.$(k∈Z),且z=2x+y的最大值为6,则k的值为( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
7.如果θ是第三象限的角,那么( )
| A. | sinθ>0 | B. | cosθ>0 | C. | tanθ>0 | D. | 以上都不对 |
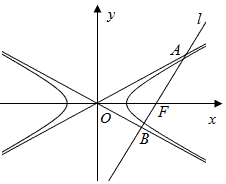 如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.
如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.