题目内容
已知曲线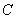 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为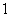 的直线和曲线
的直线和曲线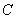 相交,另一个交点记为
相交,另一个交点记为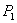 ,过
,过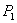 作斜率为
作斜率为 的直线与曲线
的直线与曲线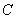 相交,另一个交点记为
相交,另一个交点记为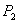 ,过
,过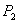 作斜率为
作斜率为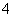 的直线与曲线
的直线与曲线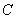 相交,另一个交点记为
相交,另一个交点记为 ,……,如此下去,一般地,过点
,……,如此下去,一般地,过点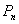 作斜率为
作斜率为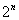 的直线与曲线
的直线与曲线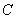 相交,另一个交点记为
相交,另一个交点记为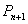 ,设点
,设点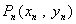 (
(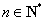 ).
).
(1)指出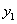 ,并求
,并求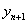 与
与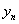 的关系式(
的关系式(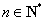 );
);
(2)求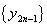 (
(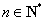 )的通项公式,并指出点列
)的通项公式,并指出点列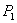 ,
, ,…,
,…,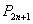 ,… 向哪一点无限接近?说明理由;
,… 向哪一点无限接近?说明理由;
(3)令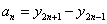 ,数列
,数列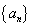 的前
的前 项和为
项和为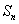 ,设
,设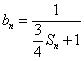 ,求所有可能的乘积
,求所有可能的乘积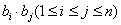 的和.
的和.
试题解析:(1)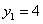 . …………………………………………………………(1分)
. …………………………………………………………(1分)
设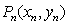 ,
,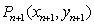 ,由题意得
,由题意得 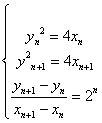 . …………(2分)
. …………(2分)
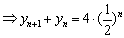 …………………(4分)
…………………(4分)


………
矩阵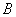 中第
中第 行的各数和
行的各数和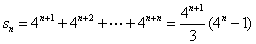 ,………(15分)从而矩阵
,………(15分)从而矩阵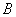 中的所有数之和为
中的所有数之和为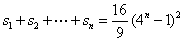 . ………………(16分)所有可能的乘积
. ………………(16分)所有可能的乘积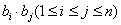 的和
的和
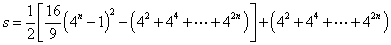
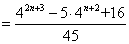 . ………………………………………………(18分)
. ………………………………………………(18分)
考点:(1)直线与抛物线相交,数列的递推关系;(2)数列的通项公式;(3)分组求和.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
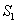 ,外接圆面积为
,外接圆面积为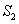 ,则
,则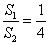 .推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为
.推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为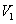 ,外接球体积为
,外接球体积为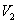 ,则
,则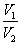 =___________.
=___________.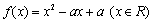 同时满足:①不等式
同时满足:①不等式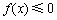 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在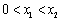 ,使得不等式
,使得不等式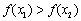 成立.设数列
成立.设数列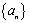 的前
的前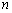 项和为
项和为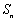 ,且
,且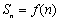 .规定:各项均不为零的数列
.规定:各项均不为零的数列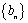 中,所有满足
中,所有满足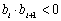 的正整数
的正整数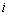 的个数称为这个数列
的个数称为这个数列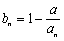 (
(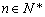 ),则数列
),则数列 ,
, ,
, ,已知
,已知 ,
, ,
, ,
, ,
, ,
, (
( ).
). 的通项公式;
的通项公式; ,
, 为定值;
为定值; ,求实数
,求实数 的取值范围.
的取值范围. ___________.
___________. = .
= .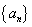 中,
中,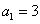 ,
,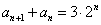 ,
, .
.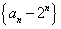 是等比数列,并求数列
是等比数列,并求数列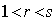 且
且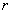 ,
,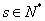 ,求证:使得
,求证:使得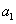 ,
,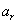 ,
, 成等差数列的点列
成等差数列的点列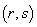 在某一直线上.
在某一直线上.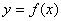 的定义域为
的定义域为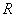 ,若存在常数
,若存在常数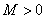 ,使得
,使得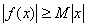 对一切实数
对一切实数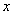 均成立,则称
均成立,则称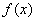 为“圆锥托底型”函数.
为“圆锥托底型”函数.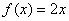 ,
, 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由. 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出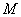 的最大值.
的最大值.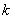 、
、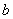 满足什么条件,
满足什么条件,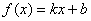 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.