题目内容
已知数列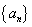 中,
中,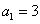 ,
,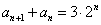 ,
, .
.
(1)证明数列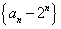 是等比数列,并求数列
是等比数列,并求数列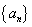 的通项公式;
的通项公式;
(2)在数列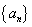 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若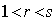 且
且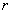 ,
,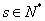 ,求证:使得
,求证:使得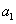 ,
,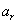 ,
, 成等差数列的点列
成等差数列的点列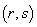 在某一直线上.
在某一直线上.

(2)假设在数列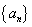 中存在连续三项成等差数列,不妨设连续的三项依次为
中存在连续三项成等差数列,不妨设连续的三项依次为 ,
, ,
, (
(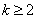 ,
,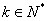 ),由题意得,
),由题意得, ,
,
将 ,
, ,
, 代入上式得……7分
代入上式得……7分
 ………………8分
………………8分
化简得, ,即
,即 ,得
,得 ,解得
,解得
所以,存在满足条件的连续三项为 ,
, ,
, 成等比数列。……10分
成等比数列。……10分


练习册系列答案
相关题目
 的实部和虚部互为相反数,那么b等于
的实部和虚部互为相反数,那么b等于 B.
B.  C.
C.  D.
D. 
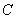 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为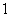 的直线和曲线
的直线和曲线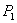 ,过
,过 的直线与曲线
的直线与曲线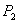 ,过
,过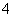 的直线与曲线
的直线与曲线 ,……,如此下去,一般地,过点
,……,如此下去,一般地,过点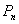 作斜率为
作斜率为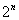 的直线与曲线
的直线与曲线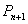 ,设点
,设点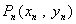 (
(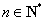 ).
).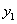 ,并求
,并求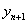 与
与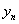 的关系式(
的关系式(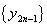 (
(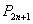 ,… 向哪一点无限接近?说明理由;
,… 向哪一点无限接近?说明理由;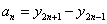 ,数列
,数列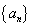 的前
的前 项和为
项和为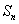 ,设
,设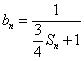 ,求所有可能的乘积
,求所有可能的乘积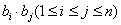 的和.
的和. 的等边三角形(图(1));二级分形图是将一级分形图的每条线段三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边(图(2));将二级分形图的每条线段三等边,重复上述的作图方法,得到三级分形图(图(3));…;重复上述作图方法,依次得到四级、五级、…、
的等边三角形(图(1));二级分形图是将一级分形图的每条线段三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边(图(2));将二级分形图的每条线段三等边,重复上述的作图方法,得到三级分形图(图(3));…;重复上述作图方法,依次得到四级、五级、…、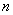 级分形图.则
级分形图.则
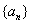 满足:
满足: ,则前6项的和
,则前6项的和 .(用数字作答)
.(用数字作答) 的首项为
的首项为 (
( ),前
),前 ,且
,且 (
( ).设
).设 ,
, (
( ).
). 时,若对任意
时,若对任意 ,
, 恒成立,求
恒成立,求 时,试求三个正数
时,试求三个正数 ,
,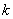 的一组值,使得
的一组值,使得 为等比数列,且
为等比数列,且
 ,则
,则 =
= B.
B. C.
C. D.
D.
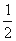
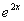 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).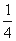
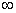 )上为增函数,求整数m 的最大值.
)上为增函数,求整数m 的最大值.