题目内容
计算: = .
= .

【解析】
试题分析:这属于“ ”型极限问题,求极限的方法是分子分母同时除以
”型极限问题,求极限的方法是分子分母同时除以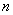 (
(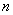 的最高次幂),化为一般可求极限型,即
的最高次幂),化为一般可求极限型,即
 .
.
考点:“ ”型极限
”型极限

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
题目内容
计算: = .
= .

【解析】
试题分析:这属于“ ”型极限问题,求极限的方法是分子分母同时除以
”型极限问题,求极限的方法是分子分母同时除以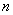 (
(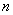 的最高次幂),化为一般可求极限型,即
的最高次幂),化为一般可求极限型,即
 .
.
考点:“ ”型极限
”型极限

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案