题目内容
已知函数f(x)=(x+1)2
(1)当1≤x≤m时,不等式f(x-3)≤x恒成立,求实数m的最大值;
(2)在曲线y=f(x+t)上存在两点关于直线y=x对称,求t的取值范围;
(3)在直线y=-
上取一点P,过点P作曲线y=f(x+t)的两条切线l1、l2,求证:l1⊥l2.
(1)当1≤x≤m时,不等式f(x-3)≤x恒成立,求实数m的最大值;
(2)在曲线y=f(x+t)上存在两点关于直线y=x对称,求t的取值范围;
(3)在直线y=-
| 1 |
| 4 |
考点:二次函数的性质
专题:函数的性质及应用,不等式的解法及应用
分析:(1)当1≤x≤m时,不等式f(x-3)≤x恒成立,即y=f(x-3)=(x-2)2在区间[1,4]上图象在直线y=x的下面,求出两个函数图象交点的坐标,可得答案.
(2)若曲线y=f(x+t)上存在两点A,B关于直线y=x对称,则方程组
有解,结合一元二次方程根的个数与△的关键,韦达定理等,可得t的取值范围;
(3)设P的坐标为(a,-
),可求出过点P作曲线y=f(x+t)的切线方程,结合切线与曲线只有一个交点,联立所得方程组只有一解,可得两条直线的斜率积为-1,进而得到结论.
(2)若曲线y=f(x+t)上存在两点A,B关于直线y=x对称,则方程组
|
(3)设P的坐标为(a,-
| 1 |
| 4 |
解答:
解:(1)∵函数f(x)=(x+1)2
∴f(x-3)=(x-2)2
由
得
或
即y=f(x-3)=(x-2)2在区间[1,4]上图象在直线y=x的下面,
即f(x-3)≤x恒成立,
∴m的最大值为4.
(2)设曲线上关于直线y=x的对称点为A(x1,y1)和B(x2,y2),线段AB的中点M(x0,y0)
则直线AB的方程为:y=-x+b
若在曲线y=f(x+t)上存在两点关于直线y=x对称,
则方程组
有解
即方程组
有解
即方程x2+(2t+3)x+(t+1)2-b=0有解
即△=(2t+3)2-4[(t+1)2-b]=4t+5+4b>0…①
则x1+x2=-2t-3,x0=-
,y0=-x0+b=
+b
又因为AB中点在直线y=x上,所以y0=x0,
得b=-2t-3
代入①式得:t<-
证明:(3)设P的坐标为(a,-
),过P的切线方程为:y+
=k(x-a),
则方程组
有且只有一解
即方程组
有且只有一解
即方程x2+[2(t+1)-k]x+(t+1)2+ka+
=0有一解
即△=[2(t+1)-k]2-4[(t+1)2+ka+
]=k2-4(t+1+a)k-1=0
直线l1、l2的斜率k1、k2为方程k2-4(t+1+a)k-1=0的两根,
则k1•k2=-1
∴l1⊥l2.
∴f(x-3)=(x-2)2
由
|
|
|
即y=f(x-3)=(x-2)2在区间[1,4]上图象在直线y=x的下面,
即f(x-3)≤x恒成立,
∴m的最大值为4.
(2)设曲线上关于直线y=x的对称点为A(x1,y1)和B(x2,y2),线段AB的中点M(x0,y0)
则直线AB的方程为:y=-x+b
若在曲线y=f(x+t)上存在两点关于直线y=x对称,
则方程组
|
即方程组
|
即方程x2+(2t+3)x+(t+1)2-b=0有解
即△=(2t+3)2-4[(t+1)2-b]=4t+5+4b>0…①
则x1+x2=-2t-3,x0=-
| 2t+3 |
| 2 |
| 2t+3 |
| 2 |
又因为AB中点在直线y=x上,所以y0=x0,
得b=-2t-3
代入①式得:t<-
| 7 |
| 4 |
证明:(3)设P的坐标为(a,-
| 1 |
| 4 |
| 1 |
| 4 |
则方程组
|
即方程组
|
即方程x2+[2(t+1)-k]x+(t+1)2+ka+
| 1 |
| 4 |
即△=[2(t+1)-k]2-4[(t+1)2+ka+
| 1 |
| 4 |
直线l1、l2的斜率k1、k2为方程k2-4(t+1+a)k-1=0的两根,
则k1•k2=-1
∴l1⊥l2.
点评:本题考查的知识点是二次函数的图象和性质,直线的交点,曲线的切线,韦达定理,直线垂直的充要条件,是函数与解析几何的综合应用,难度较大,属于难题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
在正方体ABCD-A1B1C1D1中,M,N分别C1D1,BC是的中点,则下列判断正确的是( )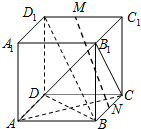

| A、MN∥BD1 |
| B、MN⊥AB1 |
| C、MN∥平面BDD1 |
| D、MN⊥平面AB1C |