题目内容
3．命题“?x∈R，x2-4＜0或x2-4x＞0”的否定为（ ）| A． | ?x∈R，x2-4≥0或x2-4x≤0 | B． | ?x∈R，x2-4≥0且x2-4x≤0 | ||
| C． | ?x∈R，x2-4≥0或x2-4x≤0 | D． | ?x∈R，x2-4≥0且x2-4x≤0 |
分析 利用特称命题的否定是全称命题，写出结果即可．
解答 解：特称命题的否定是全称命题，还需将结论否定，“或“的否定是“且”，
故命题?x∈R，x2-4＜0或x2-4x＞0”的否定为?x∈R，x2-4≥0且x2-4x≤0．
故选：B．
点评 本题考查命题的否定，特称命题与全称命题的否定关系，考查计算能力．
练习册系列答案
相关题目
14．若α∈（0，π），且3cos2α=sin（$\frac{π}{4}$-α），则sin2α的值为（ ）
| A． | 1或-$\frac{17}{18}$ | B． | $\frac{17}{18}$ | C． | 1 | D． | $-\frac{17}{18}$ |
11．已知$a={2^{\frac{6}{5}}}，b={（{\frac{1}{8}}）^{-\frac{4}{5}}}，c=2{log_5}2$，则a，b，c的大小关系为（ ）
| A． | c＜b＜a | B． | c＜a＜b | C． | b＜a＜c | D． | b＜c＜a |
18．如图所示，运行流程图，则输出的n的值等于（ ）
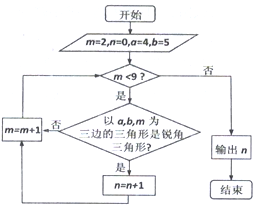
| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
8．直线y=kx+3被圆（x-2）2+（y-3）2=4截得的弦长为$2\sqrt{3}$，则直线的斜率为（ ）
| A． | $\sqrt{3}$ | B． | $±\sqrt{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $±\frac{{\sqrt{3}}}{3}$ |
如图所示，正方体 ABCD-A1B1C1D1中，M．N分别为棱 C1D1，C1C的中点，有以下四个结论：①直线AM与C1C是相交直线；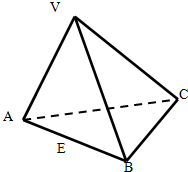 
三棱锥V-ABC中，VA=VB=AC=BC=2，AB=2$\sqrt{3}$，VC=1，E为AB边中点．