题目内容
在半径为1的圆周上任取三点,连接成三角形,这个三角形是锐角三角形的概率是多少?
考点:几何概型
专题:计算题,概率与统计
分析:根据题意,将圆周按逆时针方向依次标记三点为A、B、C,设出弧AB、弧BC与弧CA的长度,得到所有可能的结果构成的平面区域与“三点组成锐角三角形”构成的平面区域,分别算出两个区域的面积再利用几何概型公式加以计算,可得能构成锐角三角形的概率.
解答:
解:如图①,按逆时针方向依次标记三点为A、B、C,设弧AB=x,弧BC=y,弧CA=2π-x-y.

依题意,所有可能的结果构成平面区域为:Ω={(x,y)|0<x<2π,0<y<2π,0<2π-x-y<2π}.
事件A=“三点组成锐角三角形”构成的平面区域为:A={(x,y)∈Ω|0<x<π,0<y<π,0<2π-x-y<π}.
分别作出Ω与A中不等式组对应的平面区域,得到两个三角形及其内部区域,如图②所示
∵平面区域Ω的面积为μΩ=
×2π×2π=2π2,平面区域A的面积为μA=
×π×π=
π2,
∴故所求概率为P(A)=
=
=
.
答:这个三角形是锐角三角形的概率是
.

依题意,所有可能的结果构成平面区域为:Ω={(x,y)|0<x<2π,0<y<2π,0<2π-x-y<2π}.
事件A=“三点组成锐角三角形”构成的平面区域为:A={(x,y)∈Ω|0<x<π,0<y<π,0<2π-x-y<π}.
分别作出Ω与A中不等式组对应的平面区域,得到两个三角形及其内部区域,如图②所示
∵平面区域Ω的面积为μΩ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴故所求概率为P(A)=
| μA |
| μΩ |
| ||
| 2π2 |
| 1 |
| 4 |
答:这个三角形是锐角三角形的概率是
| 1 |
| 4 |
点评:本题给出圆周上的任意三点,求此三点能构成锐角三角形的概率,着重考查了圆内接三角形、二元一次不等式组表示的平面区域和几何概型计算公式等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
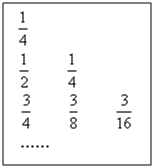 如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )
如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )A、
| ||
B、
| ||
C、
| ||
D、
|
不等式
≥3的解集为 ( )
| 2x+1 |
| x |
| A、[-1,0) |
| B、[-1,+∞) |
| C、(0,1] |
| D、(-∞,-1]∪(0,+∞) |
三个数0.993.3,log3π,log20.8的大小关系为( )
| A、log3π<0.993.3<log20.8 |
| B、log20.8<log3π<0.993.3 |
| C、log20.8<0.993.3<log3π |
| D、0.993.3<log20.8 l<log3π |