题目内容
5.将函数y=$\sqrt{3}cosx+sinx({x∈R})$的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
分析 函数解析式提取2变形后,利用两角和与差的正弦函数公式化为一个角的正弦函数,利用平移规律得到平移后的解析式,根据所得的图象关于y轴对称,即可求出m的最小值.
解答 解:y=$\sqrt{3}$cosx+sinx=2($\frac{\sqrt{3}}{2}$cosx+$\frac{1}{2}$sinx)=2sin(x+$\frac{π}{3}$),
∴图象向左平移m(m>0)个单位长度得到y=2sin[(x+m)+$\frac{π}{3}$]=2sin(x+m+$\frac{π}{3}$),
∵所得的图象关于y轴对称,
∴m+$\frac{π}{3}$=kπ+$\frac{π}{2}$(k∈Z),
由于m>0,则m的最小值为$\frac{π}{6}$.
故选:A.
点评 此题考查了两角和与差的正弦函数公式,以及函数y=Asin(ωx+φ)的图象变换,熟练掌握公式是解本题的关键,属于基础题.

练习册系列答案
相关题目
17.在等比数列{an}中,3a5-a3a7=0,若数列{bn}为等差数列,且b5=a5,则{bn}的前9项的和S9为( )
| A. | 24 | B. | 25 | C. | 27 | D. | 28 |
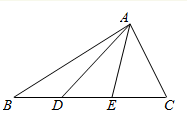 如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.
如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.